HY8:Hydraulic Jump Calculations

Determining if a Hydraulic Jump Exists and its Location

A hydraulic jump is rapidly varied flow where supercritical flow rapidly becomes subcritical flow. As the flow performs this change, energy is lost to turbulence. However, momentum is conserved across the jump. The depth of the flow just prior and after a hydraulic jump is called sequent depths, and thus by definition conserve momentum, but not energy. Sequent depths then can be used to compare the momentum of a supercritical depth to a subcritical depth.

To determine if a hydraulic jump exists, one must determine the supercritical and subcritical water surface profiles that can form within a channel or culvert. Then at each location along the two profiles compare the sequent depth of the supercritical profile to the subcritical profile’s depth. If the sequent depth matches the depth of the subcritical profile, then a hydraulic jump is assumed to occur at that location.

First, HY-8 determines the boundary conditions for the direct step method. HY-8 then computes two flow profiles from the given boundary conditions in the culvert. One profile begins at the inlet and travels downstream and is supercritical. The second profile begins at the outlet and travels upstream and is subcritical. HY-8 uses the energy equation to determine the hydraulic grade line if the outlet is submerged. Once the hydraulic grade line falls below the crown of the culvert, HY-8 uses the direct step method to determine the remainder of the profile.

HY-8 also determines the sequent depth of the supercritical flow profile. The equations used to determine the sequent depth vary by shape and are detailed in Nathan Lowe’s thesis (Lowe, 2008).

An example of a profile set and sequent depth calculations from a box culvert is given in Table 1 and plotted in Figure 1. The subcritical depth is shown extending above the crown of the culvert to show the hydraulic grade line for comparison purposes. Once HY-8 concludes the hydraulic jump calculations, the flow profile is modified to be contained within the culvert barrel.

Table 1: Parameters of culvert used for example

Parameter	Value	Units
Culvert Shape	Box
Rise:	6.0	ft
Span:	6.0	ft
Length:	100.0	ft
Flow:	80.0	cfs

Table 2: HY-8 Water Surface Profile and Sequent Depth Calculations

Computation Direction: Upstream to Downstream
Location (ft)	S2 Water Depth (ft)	Sequent Depth (ft)
0	1.767423128	1.767423128
0.029316423	1.717423128	1.818384336
0.121221217	1.667423128	1.871344458
0.284143628	1.617423128	1.926427128
0.528025114	1.567423128	1.983769228
0.86466911	1.517423128	2.043522893
1.308192917	1.467423128	2.105857905
1.87561876	1.417423128	2.17096453
2.587657601	1.367423128	2.239056945
3.469764745	1.317423128	2.310377355
4.553586554	1.267423128	2.385201009
5.878983069	1.217423128	2.463842333
7.496921363	1.167423128	2.546662495
9.473726216	1.117423128	2.634078814
11.89752361	1.067423128	2.726576563
14.88838	1.017423128	2.824723925
18.61499626	0.967423128	2.929191151
23.32377651	0.917423128	3.040775386
29.3931714	0.867423128	3.160433253
37.44519272	0.817423128	3.289324251
48.60550709	0.767423128	3.42886946
65.23610698	0.717423128	3.580832395
93.76009585	0.667423128	3.747432593
100	0.663122364	3.762533062

Computation Direction: Downstream to Upstream
Location (ft)	S1 Water Depth (ft)
100	7.78884205
76.62538619	6
76.01536408	5.95
75.40596369	5.9
74.79697048	5.85
74.18839865	5.8
73.58026305	5.75
72.97257915	5.7
72.36536314	5.65
71.75863195	5.6
71.15240324	5.55
70.54669552	5.5
69.94152813	5.45
69.33692135	5.4
68.73289638	5.35
68.12947544	5.3
67.52668185	5.25
66.92454003	5.2
66.3230756	5.15
65.72231547	5.1
65.12228788	5.05
64.5230225	5
63.92455054	4.95
63.32690478	4.9
62.73011975	4.85
62.13423177	4.8
61.5392791	4.75
60.94530208	4.7
60.35234323	4.65
59.76044741	4.6
59.16966197	4.55
58.58003695	4.5
57.9916252	4.45
57.40448266	4.4
56.81866848	4.35
56.23424533	4.3
55.6512796	4.25
55.06984171	4.2
54.49000634	4.15
53.91185285	4.1
53.33546552	4.05
52.76093401	4
52.18835372	3.95
51.61782627	3.9
51.04946001	3.85
50.48337049	3.8
49.91968113	3.75
49.35852381	3.7
48.80003962	3.65
48.24437962	3.6
47.69170569	3.55
47.1421915	3.5
46.59602356	3.45
46.05340235	3.4
45.51454362	3.35
44.97967983	3.3
44.44906168	3.25
43.92295991	3.2
43.40166723	3.15
42.88550053	3.1
42.37480328	3.05
41.86994835	3
41.37134098	2.95
40.87942233	2.9
40.39467334	2.85
39.91761912	2.8
39.44883402	2.75
38.98894719	2.7
38.53864914	2.65
38.09869903	2.6
37.66993312	2.55
37.25327445	2.5
36.84974393	2.45
36.46047324	2.4
36.08671965	2.35
35.72988334	2.3
35.39152756	2.25
35.07340226	2.2
34.77747182	2.15
34.50594783	2.1
34.26132798	2.05
34.04644235	2
33.86450893	1.95
33.71920038	1.9
33.61472501	1.85
33.55592549	1.8

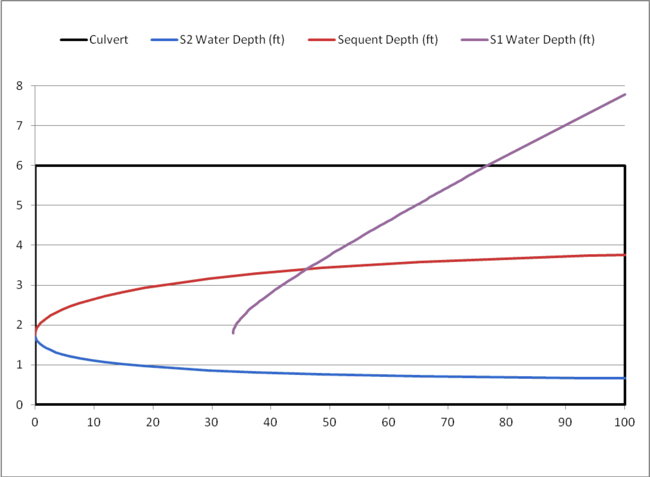Figure 1: HY-8 Water Surface Profile and Sequent Depth Calculations

In Figure 1, the sequent depth shown in the red line crosses the S1 water depth shown in the purple line. This shows that a hydraulic jump occurs and is located at approximately 46’ downstream of the inlet of the culvert. The water surface profile is then stitched together from the two profiles. If we assume that the length of the hydraulic jump is zero, the jump would be a vertical line. An example of a water surface profile for a hydraulic jump assuming zero jump length is shown in Figure 2.

Figure 2: Water Surface Profile Assuming a Jump Length of Zero

Now that HY-8 has determined that a jump occurs and where, HY-8 needs to determine the length of the jump and apply that length to the slope change. This will smooth out the plot.

Determining the Length of a Hydraulic Jump

We use the equation determined by Bradley and Peterka in 1957 as shown in Equation 1. This equation requires the upstream Froude number and the downstream depth.

File:JumpLength.png (Equation 1)

HY-8 determines the length of the jump and modifies the profile to an angled transition to the subcritical flow rather than a vertical transition. The beginning of the jump is assumed to be the location previously determined as the jump location. The end of the jump is the beginning of the jump plus the jump length. If the end of the jump is outside of the culvert, the jump is assumed to be swept out. This may or may not happen, but is considered to be conservative. This assumption means HY-8 report less hydraulic jumps than will occur. An example of hydraulic jump length calculations is shown in Table 3. The profile showing the hydraulic jump with the jump length applied is shown in Figure 3.

Table 3: Hydraulic Jump Length Calculations

Parameter	Value	Units
Culvert Shape	Box
Froude Number 1:	3.4229
Depth 1:	0.7778	ft
Length of Jump:	18.77	ft
Station 1:	46.0	ft
Station 2:	64.8	ft

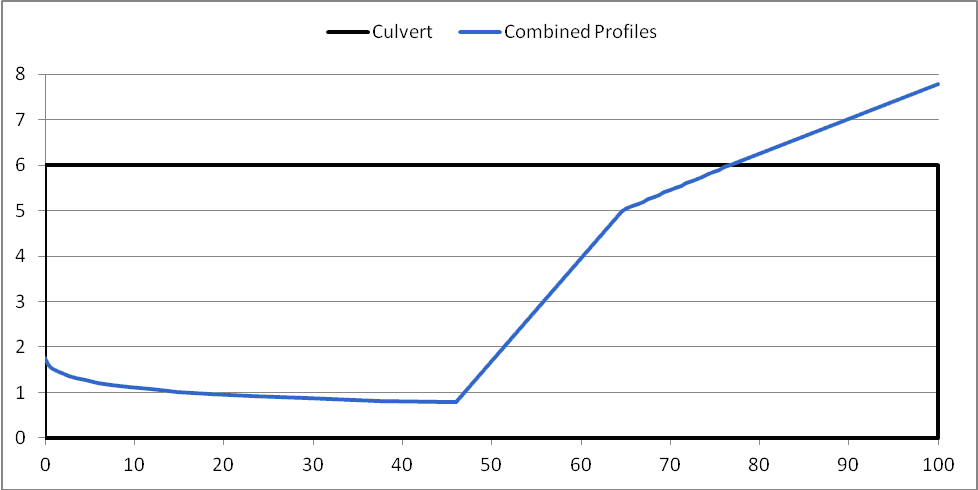Figure 3: Water Profile with Hydraulic Jump with Calculated Jump Length

When HY-8 finishes computing the hydraulic jump length, and has applied it to the profile, HY-8 trims the profile to stay within the culvert barrel. The completed profile is shown in Figure 4.

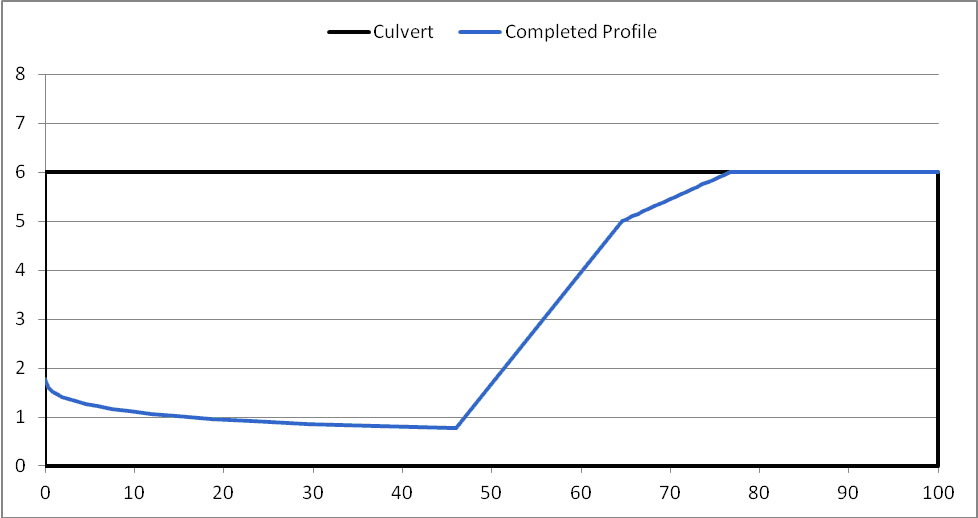Figure 4: Completed Water Surface Profile

References

Lowe, N. J. (2008). THEORETICAL DETERMINATION OF SUBCRITICAL SEQUENT DEPTHS FOR COMPLETE AND INCOMPLETE HYDRAULIC JUMPS IN CLOSED CONDUITS OF ANY SHAPE. Provo, Utah: Brigham Young University.