SMS:LTEA
Linear Truncation Error Analysis (LTEA) Toolbox incorporated into SMS uses the LTEA algorithm as the heart of a utility which creates finite element meshes of varying resolution for ADCIRC analysis. The algorithm was initially presented by Dr. Scott C. Hagen as part of his doctoral research at Notre Dame, and development has continued on the methodology at the University of Central Florida. It performs analysis on an existing ADCIRC mesh and its solution to help quantify the error associated with the mesh. Normally, this ADCIRC solution is taken from a "linear ADCIRC" run. This type of run is used to make the process faster and to simplify the LTEA algorithm applied to the unstructured mesh. A second phase of the LTEA process uses the error values at each node to create a relative size function covering the domain called DelX. This refines the mesh where the element error values would be greatest such as near shorelines or around islands.
The LTEA Toolbox
SMS includes a graphical interface that allows using the LTEA theory to guide the generation of a finite element mesh. The tool requires two inputs which must be loaded into SMS. These include:
- A bathymetry scatter set.
- An ADCIRC coverage having at least one polygon with the boundary conditions assigned.
If wanting to start the mesh generation process from an existing ADCIRC mesh, convert the mesh to both a scatter set and ADCIRC conceptual model, Right-clicking on the mesh in the project explorer gives access to commands to perform the basic conversion. The conceptual model must be defined on the arcs created in this way.
The toolbox is accessed through the Mesh Generation Toolbox... from the ADCIRC menu in the Mesh Module. From the dialog that appears, select the LTEA option and click Run. The steps that follow include:
- Step 1 – Linear Run Mesh generation. In this step specify the scatter set and conceptual model to be used for mesh generation. This step generates a basic mesh from the conceptual model to perform a linear run. This mesh may be saved for future reference. If a mesh already exists that is suitable for the linear run, the option to generate a linear run mesh should be turned off.
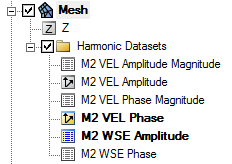
- Step 2 – Linear ADCIRC Run. In this step, the toolbox runs ADCIRC in linear mode with the M2 tidal constituent and performs an harmonic analysis on the result. If a run of ADCIRC and harmonic analysis has already been performed, the option to use existing solution data becomes available. In this case specify the datasets that contain the output of the harmonic analysis. If this is not the initial pass through the mesh generation toolbox, or if wanting to generate a "Size guideline function" from anaother source, it may be provided. If this is the case, the linear run as well as the next step "LTEA calculations" are bypassed.
- Step 3 – LTEA Analysis. The LTEA algorithm processes the harmonic analysis output and determines the relative error due to node spacing throughout the domain. It then computes a size guideline for generating a new mesh. The guideline is a dataset (a value for each node of the linear run mesh) named "DelX". Instruct LTEA to only perform calcualtions on the interior (no partial molecule) or to approximate the LTEA calculations right up to the boundary. (Note: extra controls exist in the dialog for tools that are under development.)
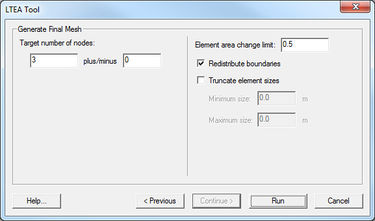
- Step 4 – Generate Final Mesh. At this point, SMS has almost all the information required for mesh generation. Specify the target size of desired mesh as a number of nodes and a tolerable deviation from that target. The acceptable size transitions are also specified here (see the Smooth Dataset article for a description of this).
The tool can be used repetitively to generate various meshes of the same area with varying resolution. In these cases, the first three steps should be bypassed by entering the input data in step 1 and the "DelX" function in step 3 and then proceeding to step 4.
LTEA Tool Overview
A set of standard buttons can be found at the bottom of the LTEA Toolbox. They are as follows:
- Help... – Launches the Help dialogue
- Continue > – Moves to next step of the LTEA Toolbox dialog.
- < Previous – Allows returning to a an earlier step in the LTEA Toolbox dialog.
- Stop and Run – Causes SMS to close the toolbox and run the LTEA analysis. The analysis generates several datasets used as size functions in the mesh generation process.
- Run – Activates the model engine at the completion of all steps.
- Cancel – Closes the LTEA Toolbox dialog without saving and information entered.
Step 1:Linear Rush Mesh
- Boundary:
- Bathymeytry:
- Create Linear Run Mesh
- Override Boundary Spacing
- Coastline Spacing
- Deep Water Spacing
- Override Boundary Spacing
- Use Current Mesh
- Save Linear Run Mesh
Step 2: IMS-ADCIRC Linear Run
- Run IMS-ADCRIC Linear Run
- Wave Continuity/Friction Coefficient:
- Minimum Angle for Tangential Flow:
- Absolute Convergence Criteria:
- Ramp Time
- Run Time:
- Time Step:
- Provide Harmonic Solutions
- Eta Ampitude:
- Eta Phase:
- Velocity Ampitude:
- Velocity Phase:
- Provide DelX
- DelX:
Step 3: LTEA Analysis
- Run Type:
- Value for dc:
- Minimum spacing from:
- Node Number:
- Use Partial molecule
- Molecule size:
Step 4:Generate Final Mesh
- Target number of nodes:
- Element area change limit:
- Redistribute boundaries
- Truncate element sizes
- Minimum Size
- Maximum Size
Case Studies / Sample Problems
Tutorials
The following tutorials may be helpful for learning to use LTEA in SMS:
- Models Section
- ADCIRC LTEA – Uses LTEA to mesh Shinnecock bay and the area around it along Long Island, NY.
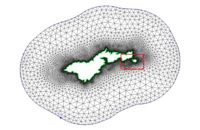
American Samoa
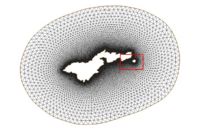
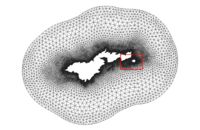
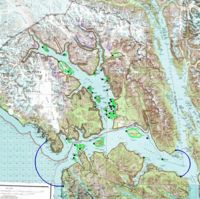
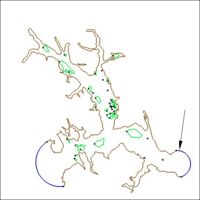
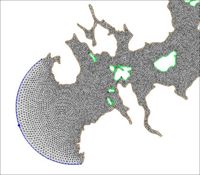
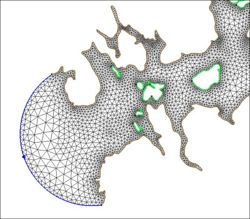
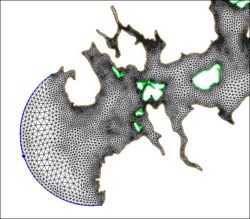
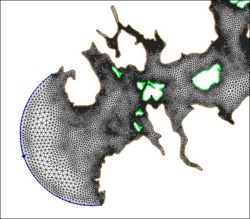
The following images illustrate the results of the LTEA toolbox applied to a domain around American Samoa. The first pair of images illustrate a mesh generated for the domain using the paving method. Density at the coastline was controlled by redistributing the vertices on the arcs representing the coastline and the density varied to a larger ocean boundary density. This mesh consists of 22,576 nodes (43,055 elements). The other images illustrate the varying resolution generated by LTEA to result in constant error with target mesh sizes of 24,000 nodes and 12,000 nodes respectively. The LTEA toolbox created meshes with 24,078 nodes (45,929 elements) and 12,029 nodes ( 22,543 elements).
These images illustrate the redistribution of density to increase the density in areas that require additional detail for solution variations, or to reduce the number of nodes in the mesh.
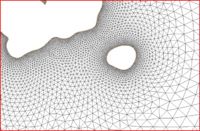
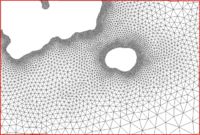
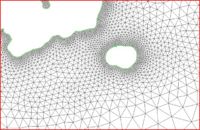
Glacier Bay Alaska
The case of Glacier Bay Alaska, by Dave F. Hill's research group, poses another problem for the LTEA toolbox. This case includes two ocean boundaries. The figures below show three meshes generated for this case and illustrate the large variation in node density that can be produced by the procedure.
This case includes two ocean boundaries. Currently, the LTEA toolbox makes a sometimes erroneous assumption that only one ocean boundary exists. To work around this problem in the current version of SMS, the following steps are required:
- Change the inland ocean boundary to land
- Run the first step of the LTEA toolbox to generate the "Linear Run Mesh" and then "Stop and Run" to that point.
- Outside of the toolbox, change the second ocean boundary to ocean on the linear run mesh and run a linear run of ADCIRC with harmonic analysis turned on. This will generate the datasets for LTEA calcuations.
- Relaunch the toolbox and select the datasets from the linear run to guide the mesh generation process.
Related Topics
External Links
- Coastal Hydroscience Analysis, Modeling & Predictive Simulations Laboratory (CHAMPS Lab)
- Sep 2006 Automatic, unstructured mesh generation for 2D, shelf-based tidal models
- Sep 2006 Automatic, unstructured mesh generation for tidal calculations in a large domain
- Sep 2006 Resolution Issues in Numerical Models of Oceanic and Coastal Circulation
- 2001 Two-dimensional, unstructured mesh generation for tidal models
- 2000 One-dimensional finite element grids based on a localized truncation error analysis
- Glacier Bay Test Case by Dave F. Hill
SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||