SMS:Natural Neighbor Interpolation: Difference between revisions
mNo edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
[[Image:Equation41.jpg]] | [[Image:Equation41.jpg]] | ||
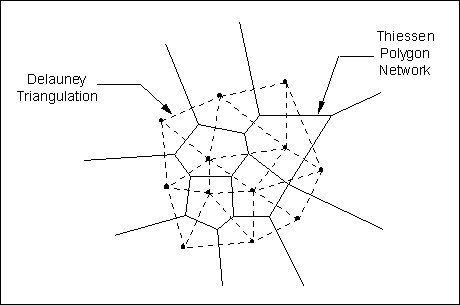
[[Image:Delauney_triangulation.jpg|frame|Delauney Triangulation and Corresponding Thiessen Polygon Network for a Set of Scatter Points.]] | |||
SMS uses nodal functions with IDW. The nodal function can be selected using the Natural Neighbor Interpolation Options dialog. The difference between IDW interpolation and natural neighbor interpolation is the method used to compute the weights and the method used to select the subset of scatter points used for interpolation. | SMS uses nodal functions with IDW. The nodal function can be selected using the Natural Neighbor Interpolation Options dialog. The difference between IDW interpolation and natural neighbor interpolation is the method used to compute the weights and the method used to select the subset of scatter points used for interpolation. | ||
Natural neighbor interpolation is based on the Thiessen polygon network of the scatter point set. The Thiessen polygon network can be constructed from the Delauney triangulation of a scatter point set. A Delauney triangulation is a TIN that has been constructed so that the Delauney criterion has been satisfied. | Natural neighbor interpolation is based on the Thiessen polygon network of the scatter point set. The Thiessen polygon network can be constructed from the Delauney triangulation of a scatter point set. A Delauney triangulation is a TIN that has been constructed so that the Delauney criterion has been satisfied. | ||
There is one Thiessen polygon in the network for each scatter point. The polygon encloses the area that is closer to the enclosed scatter point than any other scatter point. The polygons in the interior of the scatter point set are closed polygons and the polygons on the convex hull of the set are open polygons. | There is one Thiessen polygon in the network for each scatter point. The polygon encloses the area that is closer to the enclosed scatter point than any other scatter point. The polygons in the interior of the scatter point set are closed polygons and the polygons on the convex hull of the set are open polygons. | ||
| Line 22: | Line 19: | ||
==Local Coordinates== | |||
The weights used in natural neighbor interpolation are based on the concept of local coordinates. Local coordinates define the "neighborliness" or amount of influence any scatter point will have on the computed value at the interpolation point. This neighborliness is entirely dependent on the area of influence of the Thiessen polygons of the surrounding scatter points. | The weights used in natural neighbor interpolation are based on the concept of local coordinates. Local coordinates define the "neighborliness" or amount of influence any scatter point will have on the computed value at the interpolation point. This neighborliness is entirely dependent on the area of influence of the Thiessen polygons of the surrounding scatter points. | ||
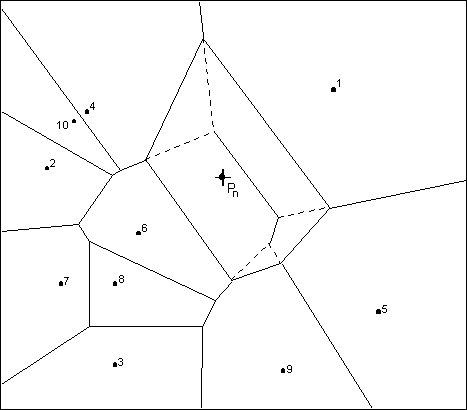
[[Image:Thiessen_polygons.jpg|frame|Overlapping Thiessen Polygon Areas Used in Computation of Local Coordinates.]] | |||
To define the local coordinates for the interpolation point, Pn, the area of all Thiessen polygons in the network must be known. Temporarily inserting Pn into the TIN causes the TIN and the corresponding Thiessen network to change, resulting in new Thiessen areas for the polygons in the neighborhood of Pn. | To define the local coordinates for the interpolation point, Pn, the area of all Thiessen polygons in the network must be known. Temporarily inserting Pn into the TIN causes the TIN and the corresponding Thiessen network to change, resulting in new Thiessen areas for the polygons in the neighborhood of Pn. | ||
The concept of local coordinates is shown graphically in the following figure. Points 1 | The concept of local coordinates is shown graphically in the following figure. Points 1–10 are scatter points and Pn is a point where some value associated with points 1–10 is to be interpolated. The dashed lines show the edges of the Thiessen network before Pn is temporarily inserted into the TIN and the solid lines show the edges of the Thiessen network after Pn is inserted. | ||
Only those scatter points whose Thiessen polygons have been altered by the temporary insertion of Pn are included in the subset of scatter points used to interpolate a value at Pn. In this case, only points 1, 4, 5, 6, & 9 are used. The local coordinate for each of these points with respect to Pn is defined as the area shared by the Thiessen polygon defined by point Pn and the Thiessen polygon defined by each point before point Pn is added. The greater the common area, the larger the resulting local coordinate, and the larger the influence or weight the scatter point has on the interpolated value at Pn. | Only those scatter points whose Thiessen polygons have been altered by the temporary insertion of Pn are included in the subset of scatter points used to interpolate a value at Pn. In this case, only points 1, 4, 5, 6, & 9 are used. The local coordinate for each of these points with respect to Pn is defined as the area shared by the Thiessen polygon defined by point Pn and the Thiessen polygon defined by each point before point Pn is added. The greater the common area, the larger the resulting local coordinate, and the larger the influence or weight the scatter point has on the interpolated value at Pn. | ||
Revision as of 19:49, 31 October 2012
Natural neighbor interpolation is also supported in SMS. Natural neighbor interpolation has many positive features. It can be used for both interpolation and extrapolation and it generally works well with clustered scatter points. Natural neighbor interpolation was first introduced by Sibson (1981). A more detailed description of natural neighbor interpolation in multiple dimensions can be found in Owen (1992).
The basic equation used in natural neighbor interpolation is identical to the one used in IDW interpolation:
SMS uses nodal functions with IDW. The nodal function can be selected using the Natural Neighbor Interpolation Options dialog. The difference between IDW interpolation and natural neighbor interpolation is the method used to compute the weights and the method used to select the subset of scatter points used for interpolation.
Natural neighbor interpolation is based on the Thiessen polygon network of the scatter point set. The Thiessen polygon network can be constructed from the Delauney triangulation of a scatter point set. A Delauney triangulation is a TIN that has been constructed so that the Delauney criterion has been satisfied.
There is one Thiessen polygon in the network for each scatter point. The polygon encloses the area that is closer to the enclosed scatter point than any other scatter point. The polygons in the interior of the scatter point set are closed polygons and the polygons on the convex hull of the set are open polygons.
Each Thiessen polygon is constructed using the circumcircles of the triangles resulting from a Delauney triangulation of the scatter points. The vertices of the Thiessen polygons correspond to the centroids of the circumcircles of the triangles.
Local Coordinates
The weights used in natural neighbor interpolation are based on the concept of local coordinates. Local coordinates define the "neighborliness" or amount of influence any scatter point will have on the computed value at the interpolation point. This neighborliness is entirely dependent on the area of influence of the Thiessen polygons of the surrounding scatter points.
To define the local coordinates for the interpolation point, Pn, the area of all Thiessen polygons in the network must be known. Temporarily inserting Pn into the TIN causes the TIN and the corresponding Thiessen network to change, resulting in new Thiessen areas for the polygons in the neighborhood of Pn.
The concept of local coordinates is shown graphically in the following figure. Points 1–10 are scatter points and Pn is a point where some value associated with points 1–10 is to be interpolated. The dashed lines show the edges of the Thiessen network before Pn is temporarily inserted into the TIN and the solid lines show the edges of the Thiessen network after Pn is inserted.
Only those scatter points whose Thiessen polygons have been altered by the temporary insertion of Pn are included in the subset of scatter points used to interpolate a value at Pn. In this case, only points 1, 4, 5, 6, & 9 are used. The local coordinate for each of these points with respect to Pn is defined as the area shared by the Thiessen polygon defined by point Pn and the Thiessen polygon defined by each point before point Pn is added. The greater the common area, the larger the resulting local coordinate, and the larger the influence or weight the scatter point has on the interpolated value at Pn.
If we define k(n) as the Thiessen polygon area of Pn and km(n) as the difference in the Thiessen polygon area of a neighboring scatter point, Pm, before and after Pn is inserted, then the local coordinate lm(n) is defined as:
The local coordinate lm(n) varies between zero and unity and is directly used as the weight, wm(n), in the interpolation equation. If Pn is at precisely the same location as Pm, then the Thiessen polygon areas for Pn and Pm are identical and lm(n) has a value of unity. In general, the greater the relative distance Pm is from Pn, the smaller its influence on the final interpolated value.
Related Topics
Modules: Mesh Module · Cartesian Grid Module · Scatter Module · Map Module · GIS Module · Particle Module
Models: ADCIRC · BOUSS-2D · CGWAVE · CMS-Flow · CMS-Wave · FESWMS · FVCOM · Generic Mesh Model · GENESIS · HYDRO AS-2D · PTM · SRH-2D · Steering · STWAVE · TABS · TUFLOW