GMS:Inverse Distance Weighted: Difference between revisions
No edit summary |
(rm table) |
||
| Line 1: | Line 1: | ||
{{3D Scatter Point links}} | {{3D Scatter Point links}} | ||
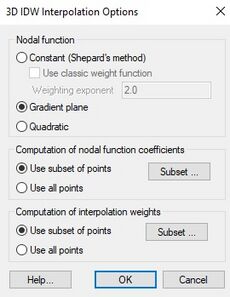
[[File:3dIDWinterpolationOpts.jpg|thumb|left|230 px|An example of the ''IDW Interpolation Options'' dialog.]] | [[File:3dIDWinterpolationOpts.jpg|thumb|left|230 px|An example of the ''IDW Interpolation Options'' dialog.]] | ||
One of the most commonly used techniques for interpolation of point data is inverse distance weighted (IDW) interpolation. Inverse distance weighted methods are based on the assumption that the interpolating surface should be influenced most by the nearby points and less by the more distant points. The interpolated surface is a weighted average of the point data; the weight assigned to each point diminishes as the distance to the interpolation location increases. Several options are available for inverse distance weighted interpolation. The options are selected using the ''IDW Interpolation Options'' dialog. This dialog is accessed through the '''Options''' button next to the Inverse distance weighted item in the ''Interpolation Options'' dialog. | |||
The options in the dialog are as follows: | The options in the dialog are as follows: | ||
| Line 10: | Line 8: | ||
*[[GMS:Quadratic Nodal Functions|Quadratic Nodal Functions]] – Makes use of quadratic polynomials to constrain nodal functions. | *[[GMS:Quadratic Nodal Functions|Quadratic Nodal Functions]] – Makes use of quadratic polynomials to constrain nodal functions. | ||
*[[GMS:Subset Definition|Subset Definition]] – Uses a subset of the data points in the computation of the nodal function coefficients and in the computation of the interpolation weights. | *[[GMS:Subset Definition|Subset Definition]] – Uses a subset of the data points in the computation of the nodal function coefficients and in the computation of the interpolation weights. | ||
{{Navbox GMS}} | {{Navbox GMS}} | ||
Revision as of 19:08, 17 April 2017
One of the most commonly used techniques for interpolation of point data is inverse distance weighted (IDW) interpolation. Inverse distance weighted methods are based on the assumption that the interpolating surface should be influenced most by the nearby points and less by the more distant points. The interpolated surface is a weighted average of the point data; the weight assigned to each point diminishes as the distance to the interpolation location increases. Several options are available for inverse distance weighted interpolation. The options are selected using the IDW Interpolation Options dialog. This dialog is accessed through the Options button next to the Inverse distance weighted item in the Interpolation Options dialog.
The options in the dialog are as follows:
- Constant Nodal Functions (Shepard's Method) – The simplest form of inverse distance weighted interpolation. Includes the option to use classic weight function by enter a weighting exponent.
- Gradient Plane Nodal Functions – Variation of Shepard's method with nodal functions or individual functions defined at each point
- Quadratic Nodal Functions – Makes use of quadratic polynomials to constrain nodal functions.
- Subset Definition – Uses a subset of the data points in the computation of the nodal function coefficients and in the computation of the interpolation weights.
| [hide] GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||