GMS:Temporal Discretization: Difference between revisions
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Many of the parameters associated with [[GMS:Feature Objects|feature objects]] can be specified as either constant or transient values. Transient values are defined as a simple list of time/data pairs using the [[:XY Series Editor|XY Series | Many of the parameters associated with [[GMS:Feature Objects|feature objects]] can be specified as either constant or transient values. Transient values are defined as a simple list of time/data pairs using the [[:XY Series Editor|''XY Series Editor'']]. The time series represents a piece-wise linear curve indicating how the parameter varies with time. When the '''Map → MODFLOW''' command is selected, these curves must undergo temporal discretization. Temporal discretization is a process of converting general time series into discrete values that apply over specific time ranges (stress periods). | ||
Transient parameters associated with feature objects are stored in an [[:XY Series Editor|xy series]]. An xy series is a general-purpose object used in GMS to represent curves of data (in this case a time series). An xy series is manipulated by GMS with regards to feature objects in three different ways: extrapolation, interpolation, and integration. | Transient parameters associated with feature objects are stored in an [[:XY Series Editor|xy series]]. An xy series is a general-purpose object used in GMS to represent curves of data (in this case a time series). An xy series is manipulated by GMS with regards to feature objects in three different ways: extrapolation, interpolation, and integration. | ||
| Line 6: | Line 7: | ||
==Interpolation== | ==Interpolation== | ||
It is also sometimes necessary to create an xy series that is a composite of two other xy series. This is the case when obtaining transient values for an intermediate point along an arc segment that has differing transient parameters at both nodes at the ends of the arc. To perform this type of interpolation, a new xy series is constructed that is the union of the x times from the two original series. The y values that correspond to each of | It is also sometimes necessary to create an xy series that is a composite of two other xy series. This is the case when obtaining transient values for an intermediate point along an arc segment that has differing transient parameters at both nodes at the ends of the arc. To perform this type of interpolation, a new xy series is constructed that is the union of the x times from the two original series. The y-values that correspond to the time step in each of the series are used to obtain a new y value for the intermediate point: | ||
<math> | <math> F=(1-h_1)y_1+(1-h_2)y_2 \,</math> | ||
Where F | Where ''F'' is the y-value along the new xy series, ''y<sub>1</sub>'' and ''y<sub>2</sub>'' are the two node xy series and ''h<sub>n</sub>'' is the interpolation weighting parameter. | ||
As an example, when one node of an arc has a constant parameter and the other has a transient parameter, the constant parameter is converted into an xy series with only one point. By using the extrapolation assumption above, it is then possible to perform a transient interpolation using two transient series. | As an example, when one node of an arc has a constant parameter and the other has a transient parameter, the constant parameter is converted into an xy series with only one point. By using the extrapolation assumption above, it is then possible to perform a transient interpolation using two transient series. | ||
==Integration== | ==Integration== | ||
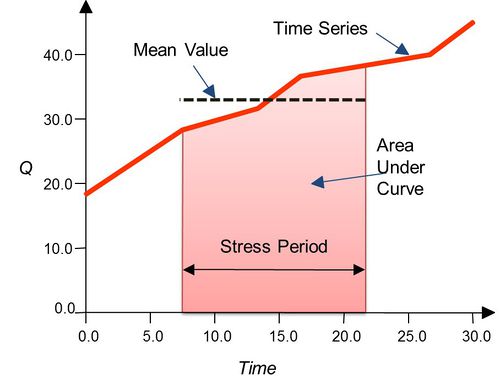
[[GMS:MODFLOW|MODFLOW]] and [[GMS:MT3DMS|MT3DMS]] both use the concept of [[GMS:Stress Periods| | [[GMS:MODFLOW|MODFLOW]] and [[GMS:MT3DMS|MT3DMS]] both use the concept of [[GMS:Stress Periods|stress periods]] to define the times that stresses may be applied. A stress period is a time interval during which all external stresses are constant. Because an xy series is not constrained to be constant over a time interval, it is necessary to obtain a representative value from the xy series that will approximate this condition. | ||
GMS uses integration of the curve defined by the xy series to obtain the average value over the stress period. This average value is then assigned to the stress period. | GMS uses integration of the curve defined by the xy series to obtain the average value over the stress period. This average value is then assigned to the stress period. | ||
| Line 25: | Line 26: | ||
==Time Units== | ==Time Units== | ||
When entering a time series in the [[GMS:Map Module|Map module]] using the [[:XY Series Editor|XY Series Editor]], | When entering a time series in the [[GMS:Map Module|Map module]] using the [[:XY Series Editor|''XY Series Editor'']], a user can use relative times (i.e., 0.0, 3.2, 5.4 etc.), or dates/times (1/1/2004 12:00:00 AM, 2/13/2004 2:01:00 PM etc.). | ||
{{Navbox GMS}} | {{Navbox GMS}} | ||
[[Category:Equations|Temporal]] | |||
[[Category:Feature Objects]] | |||
Latest revision as of 14:29, 15 August 2017
Many of the parameters associated with feature objects can be specified as either constant or transient values. Transient values are defined as a simple list of time/data pairs using the XY Series Editor. The time series represents a piece-wise linear curve indicating how the parameter varies with time. When the Map → MODFLOW command is selected, these curves must undergo temporal discretization. Temporal discretization is a process of converting general time series into discrete values that apply over specific time ranges (stress periods).
Transient parameters associated with feature objects are stored in an xy series. An xy series is a general-purpose object used in GMS to represent curves of data (in this case a time series). An xy series is manipulated by GMS with regards to feature objects in three different ways: extrapolation, interpolation, and integration.
Extrapolation
Because the user is free to enter any time values for the x parameter of an xy series, it is possible that the xy series as entered does not cover the same time range as the stress periods. In this case it may be necessary to extrapolate a value for the xy series at a time before or after the first or last entered value. In GMS the simplest approach has been used. If a value is required for a time previous to the times defined by the xy series, the first value is used. Likewise for a time that is later than the all of the times in the xy series, the last value is used. Since this behavior might hide an error in the input parameters, GMS will warn the user if any xy series does not cover the time range defined by the stress periods.
Interpolation
It is also sometimes necessary to create an xy series that is a composite of two other xy series. This is the case when obtaining transient values for an intermediate point along an arc segment that has differing transient parameters at both nodes at the ends of the arc. To perform this type of interpolation, a new xy series is constructed that is the union of the x times from the two original series. The y-values that correspond to the time step in each of the series are used to obtain a new y value for the intermediate point:
Where F is the y-value along the new xy series, y1 and y2 are the two node xy series and hn is the interpolation weighting parameter.
As an example, when one node of an arc has a constant parameter and the other has a transient parameter, the constant parameter is converted into an xy series with only one point. By using the extrapolation assumption above, it is then possible to perform a transient interpolation using two transient series.
Integration
MODFLOW and MT3DMS both use the concept of stress periods to define the times that stresses may be applied. A stress period is a time interval during which all external stresses are constant. Because an xy series is not constrained to be constant over a time interval, it is necessary to obtain a representative value from the xy series that will approximate this condition.
GMS uses integration of the curve defined by the xy series to obtain the average value over the stress period. This average value is then assigned to the stress period.
Time Units
When entering a time series in the Map module using the XY Series Editor, a user can use relative times (i.e., 0.0, 3.2, 5.4 etc.), or dates/times (1/1/2004 12:00:00 AM, 2/13/2004 2:01:00 PM etc.).
GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||