SMS:Mesh Quality: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[Image:Mesh Quality. | [[Image:Mesh Quality.png|thumb|275 px|Mesh Module ''Element Quality Checks'' dialog]] | ||
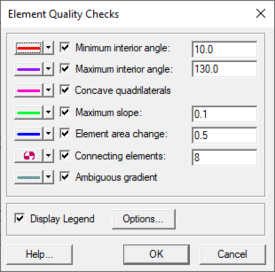
In the ''Mesh'' tab of the ''Display Options'' dialog. selecting the '''Options...''' button next to the ''Mesh Quality'' toggle will bring up the ''Element Quality Checks'' dialog. Several rules of mesh element construction, if adhered to, will help in creation of a well-behaved finite element network. Violations of the following mesh quality checks should be avoided. Violations of these mesh quality checks can be displayed in SMS (see [[SMS:Mesh_Display_Options|Mesh Display Options]]): | In the ''Mesh'' tab of the ''Display Options'' dialog. selecting the '''Options...''' button next to the ''Mesh Quality'' toggle will bring up the ''Element Quality Checks'' dialog. Several rules of mesh element construction, if adhered to, will help in creation of a well-behaved finite element network. Violations of the following mesh quality checks should be avoided. Violations of these mesh quality checks can be displayed in SMS (see [[SMS:Mesh_Display_Options|Mesh Display Options]]): | ||
* ''Minimum / Maximum interior angle'' – For triangular elements, if the angle is between 10 and 150 degrees, computation problems will usually be avoided. Care must also be taken when curved edges are defined (non-linear midside nodes) to prevent overlap of element sides. | * ''Minimum / Maximum interior angle'' – For triangular elements, if the angle is between 10 and 150 degrees, computation problems will usually be avoided. Care must also be taken when curved edges are defined (non-linear midside nodes) to prevent overlap of element sides. | ||
* ''Concave quadrilaterals'' – For quadrilateral elements, if the angle is between 30 and 150 degrees, computation problems will usually be avoided. Care must also be taken when curved edges are defined (non-linear midside nodes) to prevent overlap of element sides. | * ''Concave quadrilaterals'' – For quadrilateral elements, if the angle is between 30 and 150 degrees, computation problems will usually be avoided. Care must also be taken when curved edges are defined (non-linear midside nodes) to prevent overlap of element sides. | ||
* ''Maximum slope'' – Rapid changes in slope can cause computational instabilities. | * ''Maximum slope'' – Rapid changes in slope can cause computational instabilities. | ||
* ''Element area change'' – Nodes need to be more plentiful and elements smaller in areas where the solution variables (u,v, and h) change rapidly. Such areas may be located near channel or floodplain constrictions, in channel bends, or at sudden changes in bed slope. The network should be dense in the critical areas of interest. The density of a network can vary through the solution domain. Areas that are of little interest and have stable flow characteristics should not be as dense as critical areas. The size of elements needs to change gradually when moving from an area described by small elements to an area modeled with large elements, or vice versa. A rule of thumb is to keep the areas of neighboring elements within a factor of two, meaning an element is twice as big or half as big as its adjacent elements. | * ''Element area change'' – Nodes need to be more plentiful and elements smaller in areas where the solution variables (u,v, and h) change rapidly. Such areas may be located near channel or floodplain constrictions, in channel bends, or at sudden changes in bed slope. The network should be dense in the critical areas of interest. The density of a network can vary through the solution domain. Areas that are of little interest and have stable flow characteristics should not be as dense as critical areas. The size of elements needs to change gradually when moving from an area described by small elements to an area modeled with large elements, or vice versa. A rule of thumb is to keep the areas of neighboring elements within a factor of two, meaning an element is twice as big or half as big as its adjacent elements. That said, the actual check calculates length times height to determine if the area of change is too sudden. If one of the elements is a quadrilateral and the other is a triangle, the area of the quadrilateral is cut in half and the ratio between the two areas must be in the allowable range. | ||
<!--from email | |||
The area ratio check actually has another step included. If one of the elements is a quadrilateral and the other is a triangle, the area of the quadrilateral is cut in half. Then the ratio between the two areas must be in the allowable range. | |||
So, if the quality check is set at 0.5, the range is 0.5 to 2. | |||
Triangle area (A(t)) = 10 m^2 | |||
Quad area (A(q)) = 20 m^2 | |||
Comparison does A(t)/[0.5*A(q)] = 10/10 = 1.0 - this is between 0.5-2 | |||
OK | |||
However, if | |||
Triangle area (A(t)) = 11 m^2 | |||
Quad area (A(q)) = 10 m^2 | |||
Comparison does A(t)/[0.5*A(q)] = 11/5 = 2.2 - this is too large - quality error. | |||
This was a conscious choice because triangles are smaller than quads generally. --> | |||
* ''Connecting elements'' – Avoid creating "pinwheels" by limiting the number of elements connecting at a node to fewer than eight. | * ''Connecting elements'' – Avoid creating "pinwheels" by limiting the number of elements connecting at a node to fewer than eight. | ||
* ''Ambiguous gradient'' – All triangular elements are planar by their definition. However, quadrilateral elements may vary significantly from a plane. It is a good idea to construct elements as close to a plane as possible. This precludes the existence of elements whose slope, or direction of drainage is ambiguous. | * ''Ambiguous gradient'' – All triangular elements are planar by their definition. However, quadrilateral elements may vary significantly from a plane. It is a good idea to construct elements as close to a plane as possible. This precludes the existence of elements whose slope, or direction of drainage is ambiguous. | ||
* ''Display Legend'' – | * ''Display Legend'' – Checking this box will display the legend in the Graphics Window. | ||
<blockquote style="margin-top:0px; margin-bottom:0px;"> | <blockquote style="margin-top:0px; margin-bottom:0px;"> | ||
* '''Options...''' – | * '''Options...''' – Brings up the [[SMS:Map_Module_Display_Options|''Legend Options'']] dialog.</blockquote> | ||
==Related Topics== | ==Related Topics== | ||
* [[SMS:Mesh_Display_Options|Mesh Display Options]] | * [[SMS:Mesh_Display_Options|Mesh Display Options]] | ||
| Line 19: | Line 37: | ||
[[Category:SMS 2D Mesh|Q]] | [[Category:SMS 2D Mesh|Q]] | ||
[[Category:SMS Mesh Dialogs]] | [[Category:SMS Mesh Dialogs|Q]] | ||
Latest revision as of 14:52, 24 September 2019
In the Mesh tab of the Display Options dialog. selecting the Options... button next to the Mesh Quality toggle will bring up the Element Quality Checks dialog. Several rules of mesh element construction, if adhered to, will help in creation of a well-behaved finite element network. Violations of the following mesh quality checks should be avoided. Violations of these mesh quality checks can be displayed in SMS (see Mesh Display Options):
- Minimum / Maximum interior angle – For triangular elements, if the angle is between 10 and 150 degrees, computation problems will usually be avoided. Care must also be taken when curved edges are defined (non-linear midside nodes) to prevent overlap of element sides.
- Concave quadrilaterals – For quadrilateral elements, if the angle is between 30 and 150 degrees, computation problems will usually be avoided. Care must also be taken when curved edges are defined (non-linear midside nodes) to prevent overlap of element sides.
- Maximum slope – Rapid changes in slope can cause computational instabilities.
- Element area change – Nodes need to be more plentiful and elements smaller in areas where the solution variables (u,v, and h) change rapidly. Such areas may be located near channel or floodplain constrictions, in channel bends, or at sudden changes in bed slope. The network should be dense in the critical areas of interest. The density of a network can vary through the solution domain. Areas that are of little interest and have stable flow characteristics should not be as dense as critical areas. The size of elements needs to change gradually when moving from an area described by small elements to an area modeled with large elements, or vice versa. A rule of thumb is to keep the areas of neighboring elements within a factor of two, meaning an element is twice as big or half as big as its adjacent elements. That said, the actual check calculates length times height to determine if the area of change is too sudden. If one of the elements is a quadrilateral and the other is a triangle, the area of the quadrilateral is cut in half and the ratio between the two areas must be in the allowable range.
- Connecting elements – Avoid creating "pinwheels" by limiting the number of elements connecting at a node to fewer than eight.
- Ambiguous gradient – All triangular elements are planar by their definition. However, quadrilateral elements may vary significantly from a plane. It is a good idea to construct elements as close to a plane as possible. This precludes the existence of elements whose slope, or direction of drainage is ambiguous.
- Display Legend – Checking this box will display the legend in the Graphics Window.
- Options... – Brings up the Legend Options dialog.
Related Topics
SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||