GMS:Editing 2D Meshes: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
|||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 2: | Line 2: | ||
==Editing Nodes== | ==Editing Nodes== | ||
===Insert Node=== | ===Insert Node=== | ||
New nodes in a 2D mesh are created by selecting the '''Create Nodes''' tool from the [[GMS:2D Mesh Tool Palette|2D Mesh Tool Palette]] and clicking where the new node is to be located. The default parameters governing the creation of new nodes can be specified using the '''2D Mesh Settings''' command in the ''Mesh'' menu. This brings up the Node Options dialog. | New nodes in a 2D mesh are created by selecting the '''Create Nodes''' tool from the [[GMS:2D Mesh Tool Palette|2D Mesh Tool Palette]] and clicking where the new node is to be located. The default parameters governing the creation of new nodes can be specified using the '''2D Mesh Settings''' command in the ''Mesh'' menu. This brings up the ''Node Options'' dialog. | ||
===Delete Node=== | ===Delete Node=== | ||
| Line 11: | Line 11: | ||
If the ''Retriangulate voids when deleting'' item in the ''Node Options'' dialog is not set, the selected node and the elements surrounding the node are simply deleted and the resulting void is not filled in with triangles. | If the ''Retriangulate voids when deleting'' item in the ''Node Options'' dialog is not set, the selected node and the elements surrounding the node are simply deleted and the resulting void is not filled in with triangles. | ||
If the '''Confirm Deletions''' option in the ''Edit'' menu is active, GMS will | If the '''Confirm Deletions''' option in the ''Edit'' menu is active, GMS will ask to confirm each deletion. This feature is helpful in preventing accidental deletions. The ''Confirm Deletions'' item is toggled by selecting it from the menu. | ||
===Move Node=== | ===Move Node=== | ||
The coordinates of a 2D | The coordinates of a 2D mesh node can be edited by selecting the mesh node and entering the new coordinates in the edit boxes in the [[GMS:The GMS Window|''Edit Window'']]. It is also possible to drag an existing node to a new location by clicking on the node and moving the mouse with the button held down until the node is in the desired position. | ||
If the ''Snap to Grid'' option in the [[GMS:Drawing Grid Options|''Drawing Grid Options'']] dialog is set, the node will move in increments corresponding to the drawing grid. If the node being dragged is connected to one or more elements, GMS will not allow the node to be dragged to a position where one of the surrounding elements would become ill-formed. | If the ''Snap to Grid'' option in the [[GMS:Drawing Grid Options|''Drawing Grid Options'']] dialog is set, the node will move in increments corresponding to the drawing grid. If the node being dragged is connected to one or more elements, GMS will not allow the node to be dragged to a position where one of the surrounding elements would become ill-formed. | ||
| Line 24: | Line 24: | ||
Linear elements (three node triangles and four node quadrilaterals) can be converted to quadratic elements (six node triangles and eight node quadrilaterals) and vice versa by selecting the '''Convert Elements''' item from the ''Mesh'' menu. | Linear elements (three node triangles and four node quadrilaterals) can be converted to quadratic elements (six node triangles and eight node quadrilaterals) and vice versa by selecting the '''Convert Elements''' item from the ''Mesh'' menu. | ||
If there are both linear and quadratic elements in the mesh (as may be the case with a disjoint mesh), | If there are both linear and quadratic elements in the mesh (as may be the case with a disjoint mesh), a prompt will ask to specify the type of conversion desired; linear to quadratic or quadratic to linear. | ||
===Merging Triangles=== | ===Merging Triangles=== | ||
The [[GMS:Triangulation|triangulate]] operation creates a mesh composed entirely of triangles. In some cases it is desirable to have the mesh composed primarily of quadrilateral elements. Quadrilateral elements result in a more concise mesh which leads to faster solutions, and quadrilateral elements are often more stable numerically. To address this need, two options are provided for converting triangular elements to quadrilateral elements: The Merge Triangles command, the Merge/Split Tool. | The [[GMS:Triangulation|triangulate]] operation creates a mesh composed entirely of triangles. In some cases it is desirable to have the mesh composed primarily of quadrilateral elements. Quadrilateral elements result in a more concise mesh which leads to faster solutions, and quadrilateral elements are often more stable numerically. To address this need, two options are provided for converting triangular elements to quadrilateral elements: The '''Merge Triangles''' command, the '''Merge/Split''' Tool. | ||
====The Merge Triangles Command==== | ====The Merge Triangles Command==== | ||
The '''Merge Triangles''' command in the '' | The '''Merge Triangles''' command in the ''Mesh''|''Advanced'' menu can be used to automatically merge pairs of adjacent triangular elements into quadrilateral elements. It can also be found in the right-click menu if 2D Mesh elements are selected in the Graphics Window. Upon selecting the '''Merge Triangles''' command, a prompt will ask to input a minimum interior angle. This angle should be between 0° and 90°. If no elements are selected, all of the triangular elements in the mesh are then processed. If some elements have been selected, only the selected elements are processed. The conversion process works as follows: | ||
#The set of elements to be processed is traversed one element at a time. Each triangular element that is found is compared with each of its three adjacent elements. If the adjacent element is a triangle, the trapezoid formed by the triangle and the adjacent triangle is checked. | #The set of elements to be processed is traversed one element at a time. Each triangular element that is found is compared with each of its three adjacent elements. If the adjacent element is a triangle, the trapezoid formed by the triangle and the adjacent triangle is checked. | ||
#Each of the four interior angles of the trapezoid is computed and compared to a minimum interior angle. If all of the angles are greater than the user-specified minimum interior angle, then the two triangles are merged into a single quadrilateral element. | #Each of the four interior angles of the trapezoid is computed and compared to a minimum interior angle. If all of the angles are greater than the user-specified minimum interior angle, then the two triangles are merged into a single quadrilateral element. | ||
| Line 45: | Line 45: | ||
*'''The Split Quads Command''' – The '''Split Quads''' command in the ''Mesh'' menu can be used to split a group of quadrilateral elements into triangular elements. If no elements are selected, all of the quadrilateral elements in the mesh are split. If some elements have been selected, only the selected quadrilateral elements are split. | *'''The Split Quads Command''' – The '''Split Quads''' command in the ''Mesh'' menu can be used to split a group of quadrilateral elements into triangular elements. If no elements are selected, all of the quadrilateral elements in the mesh are split. If some elements have been selected, only the selected quadrilateral elements are split. | ||
*'''The Merge/Split Tool''' – The other option for splitting quadrilateral elements involves the use of the '''Merge/Split''' tool in the [[GMS:2D Mesh Tool Palette| | *'''The Merge/Split Tool''' – The other option for splitting quadrilateral elements involves the use of the '''Merge/Split''' tool in the [[GMS:2D Mesh Tool Palette|2D Mesh Tool Palette]]. If the '''Merge/Split''' tool is selected, clicking anywhere in the interior of a quadrilateral element with the mouse cursor will cause the element to be split into two triangles. The shortest diagonal through the quadrilateral is chosen as the common edge of the two new triangular elements | ||
===Refining Elements=== | ===Refining Elements=== | ||
| Line 56: | Line 56: | ||
The perimeter of the TIN resulting from the triangulation process corresponds to or approximates the convex hull of the TIN vertices. This may result in some long thin triangles or "slivers" on the perimeter of the triangulated region. There are several ways to deal with the long thin triangles. Thin triangles can be selected and deleted using the normal selection procedures. There is also an option for selecting thin triangles when the [[GMS:TIN Tool Palette|'''Select Triangles''']] tool is selected. If the ''Control'' key is held down, it is possible to drag a line with the mouse. All triangles intersecting the line are selected. Long thin triangles on the perimeter of the TIN can also be selected by selecting the '''Select Boundary Triangles''' command from the ''TINs'' menu. The '''Select Boundary Triangles''' command checks triangles on the outer boundary first. If the length ratio of the triangle is less than the critical length ratio, the triangle is selected and the triangles adjacent to the triangle are then checked. The process continues inward until none of the adjacent triangles violate the minimum length ratio. The critical length ratio for selecting thin triangles can be set by selecting the ''TINs'' | '''TIN Settings''' menu command. The length ratio is defined as the longest side of the triangle divided by the sum of the two shorter sides. | The perimeter of the TIN resulting from the triangulation process corresponds to or approximates the convex hull of the TIN vertices. This may result in some long thin triangles or "slivers" on the perimeter of the triangulated region. There are several ways to deal with the long thin triangles. Thin triangles can be selected and deleted using the normal selection procedures. There is also an option for selecting thin triangles when the [[GMS:TIN Tool Palette|'''Select Triangles''']] tool is selected. If the ''Control'' key is held down, it is possible to drag a line with the mouse. All triangles intersecting the line are selected. Long thin triangles on the perimeter of the TIN can also be selected by selecting the '''Select Boundary Triangles''' command from the ''TINs'' menu. The '''Select Boundary Triangles''' command checks triangles on the outer boundary first. If the length ratio of the triangle is less than the critical length ratio, the triangle is selected and the triangles adjacent to the triangle are then checked. The process continues inward until none of the adjacent triangles violate the minimum length ratio. The critical length ratio for selecting thin triangles can be set by selecting the ''TINs'' | '''TIN Settings''' menu command. The length ratio is defined as the longest side of the triangle divided by the sum of the two shorter sides. | ||
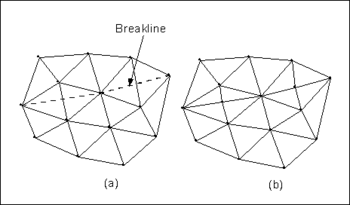
[[Image:breakline. | [[Image:breakline.png|thumb|350 px|Breaklines (a) Triangulated Mesh and Breakline. (b) Triangulated Mesh After the Breakline has been Processed.]] | ||
===Breaklines=== | ===Breaklines=== | ||
A breakline is a feature line or polyline representing a ridge or some other feature | A breakline is a feature line or polyline representing a ridge or some other feature to be preserved in a mesh made up of triangular elements. In other words, a breakline is a series of edges to which the triangles should conform to, i.e., not intersect. | ||
Breaklines can be processed using the '''Add Breaklines''' command from the ''Mesh'' menu. Before selecting the command, one or more sequences of nodes defining the breakline(s) should be selected using the '''Select Node Strings''' tool in the [[GMS:2D Mesh Tool Palette| | Breaklines can be processed using the '''Add Breaklines''' command from the ''Mesh'' menu. Before selecting the command, one or more sequences of nodes defining the breakline(s) should be selected using the '''Select Node Strings''' tool in the [[GMS:2D Mesh Tool Palette|2D Mesh Tool Palette]]. | ||
As each breakline is processed, the triangles intersected by the breakline are modified by adding new nodes at necessary locations to ensure that the edges of the triangles will conform to the breakline. The elevations of the new nodes are based on a linear interpolation of the breakline segments. The locations of the new nodes are determined in such a way that the [[GMS:Triangulation|Delauney criterion]] is satisfied. | As each breakline is processed, the triangles intersected by the breakline are modified by adding new nodes at necessary locations to ensure that the edges of the triangles will conform to the breakline. The elevations of the new nodes are based on a linear interpolation of the breakline segments. The locations of the new nodes are determined in such a way that the [[GMS:Triangulation|Delauney criterion]] is satisfied. | ||