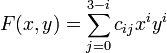GMS:Clough-Tocher: Difference between revisions
No edit summary |
(spelling) |
||
| (2 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
The Clough-Tocher interpolation technique is often referred to in the literature as a finite element method because it has origins in the finite element method of numerical analysis. Before any points are interpolated, the points are first triangulated to form a network of triangles. A bivariate polynomial is defined over each triangle, creating a surface made up of a series of triangular Clough-Tocher surface patches. | The Clough-Tocher interpolation technique is often referred to in the literature as a finite element method because it has origins in the finite element method of numerical analysis. Before any points are interpolated, the points are first triangulated to form a network of triangles. A bivariate polynomial is defined over each triangle, creating a surface made up of a series of triangular Clough-Tocher surface patches. | ||
[[Image:Cttriangle1.png|thumb|300 px|The twelve parameters used to | [[Image:Cttriangle1.png|thumb|300 px|The twelve parameters used to define the Clough-Tocher triangle]] | ||
The Clough-Tocher patch is a cubic polynomial defined by twelve parameters shown in the following figure: the function values, ''f'', and the first derivatives, ''f<sub>x</sub>'' and ''f<sub>y</sub>'', at each vertex, and the normal derivatives, ''∂f'' , at the midpoint of the three edges in the triangle (Clough & Tocher, 1965; Lancaster & Salkauskas, 1986). The first derivatives at the vertices are estimated using the average slopes of the surrounding triangles. The element is partitioned into three subelements along seams defined by the centroid and the vertices of the triangle. | The Clough-Tocher patch is a cubic polynomial defined by twelve parameters shown in the following figure: the function values, ''f'', and the first derivatives, ''f<sub>x</sub>'' and ''f<sub>y</sub>'', at each vertex, and the normal derivatives, ''∂f'' , at the midpoint of the three edges in the triangle (Clough & Tocher, 1965; Lancaster & Salkauskas, 1986). The first derivatives at the vertices are estimated using the average slopes of the surrounding triangles. The element is partitioned into three subelements along seams defined by the centroid and the vertices of the triangle. | ||
| Line 7: | Line 7: | ||
A complete cubic polynomial of the form: | A complete cubic polynomial of the form: | ||
<!-- | <!-- | ||
:<math>F(x,y) = \sum_{j=0}^{3-i}c_{ij}x^iy^i</math>--> | :<math>F(x,y) = \sum_{j=0}^{3-i}c_{ij}x^iy^i</math>--> | ||
[[Image:cloughtocher1.jpg]] | :[[Image:cloughtocher1.jpg]] | ||
is created over each sub-triangle with slope continuity across the seams and across the boundaries of the triangle. Second derivative continuity is not maintained across the seams of the triangle. | is created over each sub-triangle with slope continuity across the seams and across the boundaries of the triangle. Second derivative continuity is not maintained across the seams of the triangle. | ||
Latest revision as of 22:19, 20 September 2017
The Clough-Tocher interpolation technique is often referred to in the literature as a finite element method because it has origins in the finite element method of numerical analysis. Before any points are interpolated, the points are first triangulated to form a network of triangles. A bivariate polynomial is defined over each triangle, creating a surface made up of a series of triangular Clough-Tocher surface patches.
The Clough-Tocher patch is a cubic polynomial defined by twelve parameters shown in the following figure: the function values, f, and the first derivatives, fx and fy, at each vertex, and the normal derivatives, ∂f , at the midpoint of the three edges in the triangle (Clough & Tocher, 1965; Lancaster & Salkauskas, 1986). The first derivatives at the vertices are estimated using the average slopes of the surrounding triangles. The element is partitioned into three subelements along seams defined by the centroid and the vertices of the triangle.
A complete cubic polynomial of the form:
is created over each sub-triangle with slope continuity across the seams and across the boundaries of the triangle. Second derivative continuity is not maintained across the seams of the triangle.
Since the Clough-Tocher scheme is a local scheme, it has the advantage of speed. Even very large sets of points can be interpolated quickly. It also tends to give a smooth interpolating surface which brings out local trends in the dataset quite accurately.
Since the network of triangles only covers the convex hull of the points, extrapolation beyond the convex hull is not possible with the Clough-Tocher interpolation scheme. Any points outside the convex hull of the points are assigned the default extrapolation value entered at the bottom of the Interpolation Options dialog.
GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||