GMS:Editing 2D Meshes: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
| (4 intermediate revisions by 2 users not shown) | |||
| Line 27: | Line 27: | ||
===Merging Triangles=== | ===Merging Triangles=== | ||
The [[GMS:Triangulation|triangulate]] operation creates a mesh composed entirely of triangles. In some cases it is desirable to have the mesh composed primarily of quadrilateral elements. Quadrilateral elements result in a more concise mesh which leads to faster solutions, and quadrilateral elements are often more stable numerically. To address this need, two options are provided for converting triangular elements to quadrilateral elements: The Merge Triangles command, the Merge/Split Tool. | The [[GMS:Triangulation|triangulate]] operation creates a mesh composed entirely of triangles. In some cases it is desirable to have the mesh composed primarily of quadrilateral elements. Quadrilateral elements result in a more concise mesh which leads to faster solutions, and quadrilateral elements are often more stable numerically. To address this need, two options are provided for converting triangular elements to quadrilateral elements: The '''Merge Triangles''' command, the '''Merge/Split''' Tool. | ||
====The Merge Triangles Command==== | ====The Merge Triangles Command==== | ||
The '''Merge Triangles''' command in the '' | The '''Merge Triangles''' command in the ''Mesh''|''Advanced'' menu can be used to automatically merge pairs of adjacent triangular elements into quadrilateral elements. It can also be found in the right-click menu if 2D Mesh elements are selected in the Graphics Window. Upon selecting the '''Merge Triangles''' command, a prompt will ask to input a minimum interior angle. This angle should be between 0° and 90°. If no elements are selected, all of the triangular elements in the mesh are then processed. If some elements have been selected, only the selected elements are processed. The conversion process works as follows: | ||
#The set of elements to be processed is traversed one element at a time. Each triangular element that is found is compared with each of its three adjacent elements. If the adjacent element is a triangle, the trapezoid formed by the triangle and the adjacent triangle is checked. | #The set of elements to be processed is traversed one element at a time. Each triangular element that is found is compared with each of its three adjacent elements. If the adjacent element is a triangle, the trapezoid formed by the triangle and the adjacent triangle is checked. | ||
#Each of the four interior angles of the trapezoid is computed and compared to a minimum interior angle. If all of the angles are greater than the user-specified minimum interior angle, then the two triangles are merged into a single quadrilateral element. | #Each of the four interior angles of the trapezoid is computed and compared to a minimum interior angle. If all of the angles are greater than the user-specified minimum interior angle, then the two triangles are merged into a single quadrilateral element. | ||
| Line 45: | Line 45: | ||
*'''The Split Quads Command''' – The '''Split Quads''' command in the ''Mesh'' menu can be used to split a group of quadrilateral elements into triangular elements. If no elements are selected, all of the quadrilateral elements in the mesh are split. If some elements have been selected, only the selected quadrilateral elements are split. | *'''The Split Quads Command''' – The '''Split Quads''' command in the ''Mesh'' menu can be used to split a group of quadrilateral elements into triangular elements. If no elements are selected, all of the quadrilateral elements in the mesh are split. If some elements have been selected, only the selected quadrilateral elements are split. | ||
*'''The Merge/Split Tool''' – The other option for splitting quadrilateral elements involves the use of the '''Merge/Split''' tool in the [[GMS:2D Mesh Tool Palette| | *'''The Merge/Split Tool''' – The other option for splitting quadrilateral elements involves the use of the '''Merge/Split''' tool in the [[GMS:2D Mesh Tool Palette|2D Mesh Tool Palette]]. If the '''Merge/Split''' tool is selected, clicking anywhere in the interior of a quadrilateral element with the mouse cursor will cause the element to be split into two triangles. The shortest diagonal through the quadrilateral is chosen as the common edge of the two new triangular elements | ||
===Refining Elements=== | ===Refining Elements=== | ||
| Line 61: | Line 61: | ||
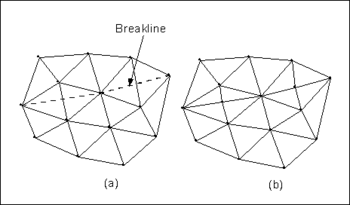
A breakline is a feature line or polyline representing a ridge or some other feature to be preserved in a mesh made up of triangular elements. In other words, a breakline is a series of edges to which the triangles should conform to, i.e., not intersect. | A breakline is a feature line or polyline representing a ridge or some other feature to be preserved in a mesh made up of triangular elements. In other words, a breakline is a series of edges to which the triangles should conform to, i.e., not intersect. | ||
Breaklines can be processed using the '''Add Breaklines''' command from the ''Mesh'' menu. Before selecting the command, one or more sequences of nodes defining the breakline(s) should be selected using the '''Select Node Strings''' tool in the [[GMS:2D Mesh Tool Palette| | Breaklines can be processed using the '''Add Breaklines''' command from the ''Mesh'' menu. Before selecting the command, one or more sequences of nodes defining the breakline(s) should be selected using the '''Select Node Strings''' tool in the [[GMS:2D Mesh Tool Palette|2D Mesh Tool Palette]]. | ||
As each breakline is processed, the triangles intersected by the breakline are modified by adding new nodes at necessary locations to ensure that the edges of the triangles will conform to the breakline. The elevations of the new nodes are based on a linear interpolation of the breakline segments. The locations of the new nodes are determined in such a way that the [[GMS:Triangulation|Delauney criterion]] is satisfied. | As each breakline is processed, the triangles intersected by the breakline are modified by adding new nodes at necessary locations to ensure that the edges of the triangles will conform to the breakline. The elevations of the new nodes are based on a linear interpolation of the breakline segments. The locations of the new nodes are determined in such a way that the [[GMS:Triangulation|Delauney criterion]] is satisfied. | ||