GMS:UGrid Inverse Distance Weighted Interpolation: Difference between revisions
(Created page with "One of the most commonly used techniques for interpolation of point data is inverse distance weighted (IDW) interpolation. Inverse distance weighted methods are based on the a...") |
No edit summary |
||
| (19 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
One of the most commonly used techniques for interpolation of point data is inverse distance weighted (IDW) interpolation. Inverse distance weighted methods are based on the assumption that the interpolating surface should be influenced most by the nearby points and less by the more distant points. The interpolated surface is a weighted average of the point data; the weight assigned to each point diminishes as the distance to the interpolation location increases. Several options are available for inverse distance weighted interpolation. The options are selected using the ''IDW Interpolation Options'' dialog. This dialog is accessed through the '''Options''' button next to the ''Inverse distance weighted'' item in the '' | [[File:Interpolate-IDW.png|thumb|300 px|The ''Interpolate – Inverse Distance Weighted'' dialog.]] | ||
One of the most commonly used techniques for interpolation of point data is inverse distance weighted (IDW) interpolation. Inverse distance weighted methods are based on the assumption that the interpolating surface should be influenced most by the nearby points and less by the more distant points. The interpolated surface is a weighted average of the point data; the weight assigned to each point diminishes as the distance to the interpolation location increases. Several options are available for inverse distance weighted interpolation. The options are selected using the ''IDW Interpolation Options'' dialog. This dialog is accessed through the '''Options''' button next to the ''Inverse distance weighted'' item in the ''Interpolate UGrid to UGrid'' dialog. | |||
The options in the dialog are as follows: | The options in the dialog are as follows: | ||
*[[GMS:Shepard's Method|Constant | *''Nodal function'' | ||
*[[GMS:Gradient Plane Nodal Functions|Gradient Plane Nodal Functions]] – Variation of Shepard's method with nodal functions or individual functions defined at each point | **[[GMS:Shepard's Method|Constant (Shepard's Method)]] – The simplest form of inverse distance weighted interpolation. Includes the option to ''Use classic weight function'' to enter a ''Weighting exponent''. | ||
*[[GMS:Quadratic Nodal Functions|Quadratic Nodal Functions]] – Makes use of quadratic polynomials to constrain nodal functions. | **[[GMS:Gradient Plane Nodal Functions|Gradient Plane Nodal Functions]] – Variation of Shepard's method with nodal functions or individual functions defined at each point | ||
* | **[[GMS:Quadratic Nodal Functions|Quadratic Nodal Functions]] – Makes use of quadratic polynomials to constrain nodal functions. | ||
*''Computation of nodal function coefficients'' – Uses a subset of the data points. Using a subset of the data points drops distant points from consideration since they are unlikely to have a large influence on the nodal function. In addition, using a subset can speed up the computations since less points are involved. Two options are available for defining which points are included in the subset. In the first approach, only the nearest ''N'' points are used. In the second approach, only the nearest ''N'' points in each quadrant are used as illustrated in the figure below. The second approach may give better results if the data points tend to be clustered. | |||
*''Computation of interpolation weights'' – Uses a subset of the data points as with the ''Computation of nodal function coefficients'' section. | |||
*''Truncate values'' – This section allows for limiting the interpolated values to lie between the minimum and maximum value. | |||
**''Truncate to min/max of dataset'' – Limits the interpolated values to the minimum and maximum values in the original dataset. | |||
**''Truncate to specified range'' – Allows setting a user specified minimum and maximum value range. | |||
**''Min'' – Manually sets a minimum value. | |||
**''Max'' – Manually sets a maximum value. | |||
*'''Advanced''' – This button will open the ''Interpolate – Advanced'' dialog where options for anisotropy and extrapolation can be adjusted. | |||
[[ | ==Related Topics== | ||
* [[GMS:UGrid Interpolation|UGrid Interpolation]] | |||
{{Navbox GMS}} | |||
[[Category:UGrid|Inter]] | |||
[[Category:UGrid Dialogs|Inter]] | |||
[[Category:Interpolation|UGrid]] | |||
Latest revision as of 15:59, 12 November 2018
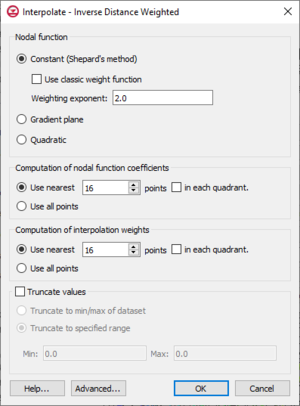
One of the most commonly used techniques for interpolation of point data is inverse distance weighted (IDW) interpolation. Inverse distance weighted methods are based on the assumption that the interpolating surface should be influenced most by the nearby points and less by the more distant points. The interpolated surface is a weighted average of the point data; the weight assigned to each point diminishes as the distance to the interpolation location increases. Several options are available for inverse distance weighted interpolation. The options are selected using the IDW Interpolation Options dialog. This dialog is accessed through the Options button next to the Inverse distance weighted item in the Interpolate UGrid to UGrid dialog.
The options in the dialog are as follows:
- Nodal function
- Constant (Shepard's Method) – The simplest form of inverse distance weighted interpolation. Includes the option to Use classic weight function to enter a Weighting exponent.
- Gradient Plane Nodal Functions – Variation of Shepard's method with nodal functions or individual functions defined at each point
- Quadratic Nodal Functions – Makes use of quadratic polynomials to constrain nodal functions.
- Computation of nodal function coefficients – Uses a subset of the data points. Using a subset of the data points drops distant points from consideration since they are unlikely to have a large influence on the nodal function. In addition, using a subset can speed up the computations since less points are involved. Two options are available for defining which points are included in the subset. In the first approach, only the nearest N points are used. In the second approach, only the nearest N points in each quadrant are used as illustrated in the figure below. The second approach may give better results if the data points tend to be clustered.
- Computation of interpolation weights – Uses a subset of the data points as with the Computation of nodal function coefficients section.
- Truncate values – This section allows for limiting the interpolated values to lie between the minimum and maximum value.
- Truncate to min/max of dataset – Limits the interpolated values to the minimum and maximum values in the original dataset.
- Truncate to specified range – Allows setting a user specified minimum and maximum value range.
- Min – Manually sets a minimum value.
- Max – Manually sets a maximum value.
- Advanced – This button will open the Interpolate – Advanced dialog where options for anisotropy and extrapolation can be adjusted.
Related Topics
GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||