SMS:Mesh Node Triangulation: Difference between revisions
mNo edit summary |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
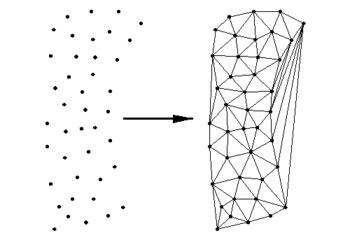
A simple means of creating a large number of elements is to triangulate a set of nodes into a network. This provides a surface that simulates the region being modeled, but normally does not result in quality elements. | A simple means of creating a large number of elements is to triangulate a set of nodes into a network. This provides a surface that simulates the region being modeled, but normally does not result in quality elements. | ||
This option is available through the Triangulate command from the Elements menu is executed. The selected nodes are connected with a series of triangles. If nodes are not selected, then all nodes will be triangulated. If linear elements exist, or a linear element creation tool has been selected, then this command creates linear triangles. Otherwise, quadratic triangles are created. | This option is available through the '''Triangulate''' command from the ''Elements'' menu is executed. The selected nodes are connected with a series of triangles. If nodes are not selected, then all nodes will be triangulated. If linear elements exist, or a linear element creation tool has been selected, then this command creates linear triangles. Otherwise, quadratic triangles are created. | ||
[[Image:TriangulateExample. | [[Image:TriangulateExample.png|350 px]] | ||
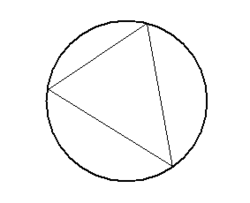
The triangulation algorithm ensures that the Delauney criterion is satisfied. The Delauney criterion is such that the circumcircle of a triangle does not enclose a node on any other element. The circumcircle of a triangle is the circle that passes through its vertices. | The triangulation algorithm ensures that the Delauney criterion is satisfied. The Delauney criterion is such that the circumcircle of a triangle does not enclose a node on any other element. The circumcircle of a triangle is the circle that passes through its vertices. | ||
[[Image:TriangleCircumcircle. | [[Image:TriangleCircumcircle.png|250 px]] | ||
==Optimize Triangulation== | ==Optimize Triangulation== | ||
At times, | At times, it's necessary to perform manual mesh editing using the '''Swap Edge''' tool. This makes the Delauney criterion no longer hold. Selected elements can be returned to the Delauney state by choosing the '''Optimize Triangulation''' command from the ''Elements'' menu. | ||
==Related Topics== | ==Related Topics== | ||
| Line 16: | Line 16: | ||
*[[SMS:2D Mesh Elements Menu|2D Mesh Elements Menu]] | *[[SMS:2D Mesh Elements Menu|2D Mesh Elements Menu]] | ||
[[Category:SMS 2D Mesh]] | {{Template:Navbox SMS}} | ||
[[Category:SMS 2D Mesh|T]] | |||
Latest revision as of 14:50, 11 May 2016
A simple means of creating a large number of elements is to triangulate a set of nodes into a network. This provides a surface that simulates the region being modeled, but normally does not result in quality elements.
This option is available through the Triangulate command from the Elements menu is executed. The selected nodes are connected with a series of triangles. If nodes are not selected, then all nodes will be triangulated. If linear elements exist, or a linear element creation tool has been selected, then this command creates linear triangles. Otherwise, quadratic triangles are created.
The triangulation algorithm ensures that the Delauney criterion is satisfied. The Delauney criterion is such that the circumcircle of a triangle does not enclose a node on any other element. The circumcircle of a triangle is the circle that passes through its vertices.
Optimize Triangulation
At times, it's necessary to perform manual mesh editing using the Swap Edge tool. This makes the Delauney criterion no longer hold. Selected elements can be returned to the Delauney state by choosing the Optimize Triangulation command from the Elements menu.
Related Topics
| [hide] SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||