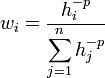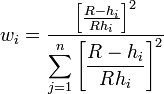GMS:Shepard's Method: Difference between revisions
No edit summary |
|||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
The simplest form of inverse distance weighted interpolation is sometimes called "Shepard's method" (Shepard 1968). The equation used is as follows: | The simplest form of inverse distance weighted interpolation is the constant nodal function sometimes called the "Shepard's method" (Shepard 1968). The equation used is as follows: | ||
<!-- | <!--<math>F(x,y) = \sum_{i=1}^n w_if_i</math>--> | ||
<math>F(x,y) = \sum_{i=1}^n w_if_i</math>--> | :[[Image:shep_eq1.jpg]] | ||
[[Image:shep_eq1.jpg]] | |||
where ''n'' is the number of points used to interpolate, ''f<sub>i</sub>'' are the prescribed function values at the points (e.g., the dataset values), and ''w<sub>i</sub>'' are the weight functions assigned to each point. The classical form of the weight function is: | where ''n'' is the number of points used to interpolate, ''f<sub>i</sub>'' are the prescribed function values at the points (e.g., the dataset values), and ''w<sub>i</sub>'' are the weight functions assigned to each point. The classical form of the weight function is: | ||
<!-- | <!--<math>w_i = \frac{h_i^{-p}}{\displaystyle \sum_{j=1}^n h_j^{-p}}</math>--> | ||
<math>w_i = \frac{h_i^{-p}}{\displaystyle \sum_{j=1}^n h_j^{-p}}</math>--> | :[[Image:shep_eq2.jpg]] | ||
[[Image:shep_eq2.jpg]] | |||
where ''p'' is an arbitrary positive real number called the weighting exponent and is defaulted to 2. The weighting exponent can be modified by turning on the ''Use classic weight function'' option. ''h<sub>i</sub>'' is the distance from the point to the interpolation location or | where ''p'' is an arbitrary positive real number called the weighting exponent and is defaulted to 2. The weighting exponent can be modified by turning on the ''Use classic weight function'' option. ''h<sub>i</sub>'' is the distance from the point to the interpolation location or | ||
<!-- | <!--<math>h_i = \sqrt{(x-x_i)^2+(y-y_i)^2}</math>--> | ||
<math>h_i = \sqrt{(x-x_i)^2+(y-y_i)^2}</math>--> | :[[Image:shep_eq3.jpg]] | ||
[[Image:shep_eq3.jpg]] | |||
where ''(x,y)'' are the coordinates of the interpolation location and ''(x<sub>i</sub>,y<sub>i</sub>)'' are the coordinates of each point. The weight function varies from a value of unity at the point to a value approaching zero as the distance from the point increases. The weight functions are normalized so that the weights sum to unity. | where ''(x,y)'' are the coordinates of the interpolation location and ''(x<sub>i</sub>,y<sub>i</sub>)'' are the coordinates of each point. The weight function varies from a value of unity at the point to a value approaching zero as the distance from the point increases. The weight functions are normalized so that the weights sum to unity. | ||
| Line 21: | Line 18: | ||
Although the weight function shown above is the classical form of the weight function in inverse distance weighted interpolation, the following equation is used in GMS: | Although the weight function shown above is the classical form of the weight function in inverse distance weighted interpolation, the following equation is used in GMS: | ||
<!-- | <!--<math>w_i = \frac{ \left [ \frac{R-h_i}{Rh_i} \right ] ^2}{\displaystyle \sum_{j=1}^n \left [ \frac{R-h_i}{Rh_i} \right ] ^2}</math>--> | ||
<math>w_i = \frac{ \left [ \frac{R-h_i}{Rh_i} \right ] ^2}{\displaystyle \sum_{j=1}^n \left [ \frac{R-h_i}{Rh_i} \right ] ^2}</math>--> | :[[Image:shep_eq4.jpg]] | ||
[[Image:shep_eq4.jpg]] | |||
where ''h<sub>i</sub>'' is the distance from the interpolation location to the point ''i'', ''R'' is the distance from the interpolation location to the most distant point, and n is the total number of points. This equation has been found to give superior results to the classical equation (Franke & Nielson, 1980). | where ''h<sub>i</sub>'' is the distance from the interpolation location to the point ''i'', ''R'' is the distance from the interpolation location to the most distant point, and n is the total number of points. This equation has been found to give superior results to the classical equation (Franke & Nielson, 1980). | ||
| Line 33: | Line 29: | ||
The 3D equations for Shepard's method are identical to the 2D equations except that the distances are computed using: | The 3D equations for Shepard's method are identical to the 2D equations except that the distances are computed using: | ||
<!-- | <!--<math>h_i = \sqrt{(x-x_i)^2+(y-y_i)^2+(z-z_i)^2}</math>--> | ||
<math>h_i = \sqrt{(x-x_i)^2+(y-y_i)^2+(z-z_i)^2}</math>--> | :[[Image:shep_eq5.jpg]] | ||
[[Image:shep_eq5.jpg]] | |||
where ''(x,y,z)'' are the coordinates of the interpolation location and ''(x<sub>i</sub>,y<sub>i</sub>,z<sub>i</sub>)'' are the coordinates of each point. | where ''(x,y,z)'' are the coordinates of the interpolation location and ''(x<sub>i</sub>,y<sub>i</sub>,z<sub>i</sub>)'' are the coordinates of each point. | ||
| Line 45: | Line 40: | ||
{{Navbox GMS}} | {{Navbox GMS}} | ||
[[Category:Interpolation]] | [[Category:Interpolation]] | ||
[[Category:Equations| | [[Category:Equations|Shepards]] | ||
Latest revision as of 13:59, 12 September 2017
The simplest form of inverse distance weighted interpolation is the constant nodal function sometimes called the "Shepard's method" (Shepard 1968). The equation used is as follows:
where n is the number of points used to interpolate, fi are the prescribed function values at the points (e.g., the dataset values), and wi are the weight functions assigned to each point. The classical form of the weight function is:
where p is an arbitrary positive real number called the weighting exponent and is defaulted to 2. The weighting exponent can be modified by turning on the Use classic weight function option. hi is the distance from the point to the interpolation location or
where (x,y) are the coordinates of the interpolation location and (xi,yi) are the coordinates of each point. The weight function varies from a value of unity at the point to a value approaching zero as the distance from the point increases. The weight functions are normalized so that the weights sum to unity.
Although the weight function shown above is the classical form of the weight function in inverse distance weighted interpolation, the following equation is used in GMS:
where hi is the distance from the interpolation location to the point i, R is the distance from the interpolation location to the most distant point, and n is the total number of points. This equation has been found to give superior results to the classical equation (Franke & Nielson, 1980).
The weight function is a function of Euclidean distance and is radially symmetric about each point. As a result, the interpolating surface is somewhat symmetric about each point and tends toward the mean value of the point data between the points. Shepard's method has been used extensively because of its simplicity.
3D Interpolation
The 3D equations for Shepard's method are identical to the 2D equations except that the distances are computed using:
where (x,y,z) are the coordinates of the interpolation location and (xi,yi,zi) are the coordinates of each point.
Related Topics
GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||