SMS:BOUSS-2D: Difference between revisions
mNo edit summary |
(No difference)
|
Revision as of 20:33, 18 March 2009
| BOUSS-2D | |
|---|---|
| Model Info | |
| Model type | Boussinesq Wave Model for Coastal Regions and Harbors. |
| Developer | Zeki Demirbilek, Ph.D. |
| Web site | BOUSS-2D web site |
| Tutorials |
General Section
Models Section
Several sets of sample problems and case studies are available. These include:
|
BOUSS-2D is based on Boussinesq-type equations derived by Okey Nwogu and has been under development since 1993. The equations are depth-integrated for the conservation of mass and momentum for nonlinear waves propagating in shallow and intermediate water depths.
Graphical Interface
The BOUSS-2D Graphical Interface contains tools to create and edit a BOUSS-2D simulation. The simulation consists of a geometric definition of the model domain (the grid) and a set of numerical parameters. The parameters define the boundary conditions and options pertinent to the model.
The interface is accessed by selecting the Cartesian Grid Module and setting the current model to BOUSS-2D. If a grid has already been created for a BOUSS-2D simulation or an existing simulation read, the grid object will exist in the Project Explorer and selecting that object will make the Cartesian grid module active and set the model to BOUSS-2D. See Creating 2D Cartesian Grids for more information.
The interface consists of the Cartesian grid menus and tools augmented by the BOUSS-2D Menu. See BOUSS-2D Graphical Interface for more information.
Functionality
BOUSS-2D computes nearshore wave fields including mean wave heights, mean current direction, mean water level breaking and transient representation of water levels, currents, and wave breaking.
BOUSS-2D is a comprehensive numerical model for simulating the propagation and transformation of waves in coastal regions and harbors based on a time-domain solution of Boussinesq-type equations. The governing equations are uniformly valid from deep to shallow water and can simulate most of the phenomena of interest in the nearshore zone and harbor basins including:
- Shoaling/refraction over variable topography
- Reflection/diffraction near structures
- Energy dissipation due to wave breaking and bottom friction
- Cross-spectral energy transfer due to nonlinear wave-wave interactions
- Breaking-induced longshore and rip currents
- Wave-current interaction
- Wave interaction with porous structures
The governing equations in BOUSS-2D are solved in the time domain with a finite-difference method. Input waves may be periodic (regular) or non-periodic (irregular), and both unidirectional or multi-directional sea states may be simulated. Waves propagating out of the computation domain are either absorbed in damping layers or allowed to leave the domain freely. The SI engineering units are used in BOUSS-2D calculations.
Output Options
The user can instruct BOUSS-2D to create a variety of output files. These may include spatially varied data consisting of a value for each cell in the grid, transient data defining time series at a location, or a combination of these two options (multiple time steps of data that includes a value at each cell). The output options, along with the keyword included in the parameter file to enable these options are shown below.
- Steady-state/single value spatially varied data sets
- Significant wave height (":HS_FILE")
- Mean currents (":MEAN_UV_FILE")
- Mean wave direction (":THETA_FILE")
- Transient spatially varied data sets. Each output includes data from a specified start time, to a specified end time at a specified time step.
- Water surface elevations (":SAVE_ETA_ANIMATION")
- Transient currents (":SAVE_UV_ANIMATION")
- Time series output at specified cells (probes). BOUSS-2D saves each type of data (for multiple locations) in a single ".ts1" file.
- Water surface elevations (":TS_ETA_FILE")
- Currents (":TS_U_FILE", ":TS_V_FILE") - This saves the current at a specified elevation up from the bed. Multiple elevations can be monitored.
- Pressure (":TS_PRESSURE_FILE") - This saves the pressure at a specified elevation up from the bed. Multiple elevations can be monitored.
- Flow rate (":TS_Q_FILE" - This saves the flow crossing a location and can be used for overtopping.
The spatially varied data may be output in to either BOUSS-2D native files or a eXtensible Data Format File (XMDF). If BOUSS-2D format is specified, the model creates "*.grd" files for each of the single value spatially varied outputs and binary data files for the transient data. The ":SOLUTION_FILE_OPTION" in the par file instructs the model to save the data in BOUSS-2D format (if set to 0), XMDF format (if set to 1) or both formats (if set to 2). When the XMDF option is specified, the ":XMDF_SOLUTION_FILE" record must also be in the parameters file along with the name of the XMDF file to store the data sets in.
Using the Model / Practical Notes
BOUSS-2D can be applied to a wide variety of coastal and ocean engineering problems, including complex wave transformation over small coastal regions (1-5 km), wave agitation and harbor resonance studies, wave breaking over submerged obstacles, breaking-induced nearshore circulation patterns, wave-current interaction near tidal inlets, infra-gravity wave generation by groups of short waves, and wave transformation around artificial islands.
As with many numerical models, BOUSS-2D can terminate or crash due to numerical instabilities. These are usually caused by problems related to the grid, the boundary conditions, or model parameters. The following lists describe common causes of instability and methods to correct them.
Instability due to the grid/geometry
- Model stability requires a low Courant number throughout the domain. SMS computes an approximate maximum timestep to maintain a Courant number below 0.5. You may want to lower the timestep even more. Additionally, you may want to truncate the computational domain to areas with depth above a specified minimum. Another option is to increase resolution by using smaller computational cells. Either of these options increase run time, so before applying them, you may want to look at the other causes of instability.
- Abrupt changes in elevation from one cell to another in the computational domain could result in instabilities. You may find it helpful to smooth the grid. (A smoothing command is available by right clicking on the grid object in the project explorer in the SMS interface.)
- Computation nodes surrounded on three or four sides by land may be created during the grid creation process. These "isolated" cells may become unstable and generally don't have an impact on the wave climate. They can be converted to land cells.
Instability due to the boundary conditions
- Generally, avoid placing damping or porosity layers along structures and shorelines.
- Wave makers are more stable on the edges of the domain. Therefore, generally speaking, the wave maker should be placed on the boundary of the domain in constant (or nearly constant) depth water. (The SMS interface offers to extend the grid and transition to constant depth if a wave maker is created in a location with more that 20% variation in depth.) This is especially true in real world applications where reflected waves are of no concern. Also, when simulating large waves, the greater stability of external wavemakers may be required.
- Wave makers should be placed far enough from shore to avoid interaction between the wave maker and reflecting waves. This is because the external boundary behind the wave maker is treated as a vertical wall.
- Exceptions, or applications in which internal wavemakers (i.e. wavemakers placed inside the domain) are recommended include:
- In applications with significant reflections from structures inside the computational domain. When reflected are caused by coastlines, structures, or bathymetry (reflected wave sources), the simulated seastate will become less uniform spatially, and the simulation may not reach a steady-state condition. The resulting wave field in such simulations will generally consist of nodes and anti-nodes that resemble a standing wave pattern, where waves appear to be bouncing back and forth inside the domain. If reflected waves cannot escape through boundaries of the modeling domain (or are constrained to exit the domain), a steady-state condition technically cannot be reached irrespective of the length of simulation. When reflected waves intercept external wavemakers, the extremes (lows and highs) in the calculated wavefield may keep building and can eventually lead to model instabilities.
- Internal wavemakers should be used for finite domains and especially for limited area physical modeling studies, and with the above specified guidance.
- If wavemakers are placed on the interior of the domain, they should cross the entire domain to avoid potential "end effects", and have a damping layer placed behind (on the seaward side of) the internal wavemakers to absorb reflected waves. There should also be a gap (at least one non-damped cell) between the internal wavemaker and the damping layer located offshore.
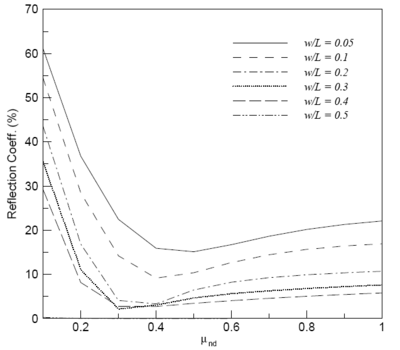
- In the absence of laboratory or field data to calibrate damping and porous layers for an application, users should consider multiple simulations with a range of damping widths and/or coefficients. This graph from BOUSS-2D's technical report illustrates the variation of effective reflectivity given various damping coefficients and damping layer widths. To use this graph:
- Compute L (the wavelength for the incident wave).
- Select a w/L ratio. Use this ratio to compute w (damping width).
- Select an expected reflection percentage. Follow a horizontal line for this percentage on plot to intersect the graph for selected w/L ratio. Read associated damping coefficient from plot.
- Note that the reflection coefficient is very sensitive to a change in damping coefficient when the coefficient is small (< 0.3) and much less sensitive when the coefficient is larger.
- This process may require the damping parameters be changed when different wave conditions are considered.
- It should be observed that this plot is for normally incident waves. Different reflection coefficients would be obtained for obliquely incident waves.
- Damping layers should be 5-10 cells wide.
Instability due to model parameters
- The model includes a Smagorinsky term to account for subgrid turbulence. If you know turbulence is expected this term can be left at the default (0.0), however, it may be increased to increase stability. (This should be done with caution. Remember, don't suppress the wiggles, they are trying to tell you something.)
External Links
- CHL BOUSS-2D website [1]
- May 2007 ERDC/CHL CHETN-I-73 Infra-Gravity Wave Input Toolbox (IGWT): User’s Guide [2]
- May 2005 ERDC/CHL CHETN-I-70 BOUSS-2D Wave Model in SMS: 2. Tutorial with Examples [3]
- Mar 2005 ERDC/CHL CHETN-I-69 BOUSS-2D Wave Model in the SMS: 1. Graphical Interface [4]
- Sep 2001 ERDC/CHL TR-1-25 BOUSS-2D: A Boussinesq Wave Model for Coastal Regions and Harbors [5]
Related Topics
Modules: Mesh Module · Cartesian Grid Module · Scatter Module · Map Module · GIS Module · Particle Module
Models: ADCIRC · BOUSS-2D · CGWAVE · CMS-Flow · CMS-Wave · FESWMS · FVCOM · Generic Mesh Model · GENESIS · HYDRO AS-2D · PTM · SRH-2D · Steering · STWAVE · TABS · TUFLOW