SMS:Scatter Options
Scatter options are accessed through the Scatter menu, Scatter Options dialog in the Scatter Module.
Triangulation Options
This section lets the user adjust the maximum aspect ratio of a thin triangle. The aspect ratio is the ratio of the triangle width to the triangle height. All triangles with an aspect ratio less than what is specified are considered thin.
Long Triangles
This section contains options for deleting or selecting long triangles.
Individual Points
This section contains the retriangulate voids when deleting option. When scatter points are deleted, the triangles attached to the scatter points (if any) are also deleted. If this option is on, surrounding triangles are retriangulated to fill the void.
Triangulation Optimization Options
When the optimize triangulation command is invoked, the triangles are optimized in one of two ways:
- Angle Optimization – The triangles are swapped to conform to the Delaunay Criterion.
- Area Optimization (SHOALS) – The triangles are swapped to align with other triangles. The swapping is done by comparing the area of one triangle to its neighbor. The user sets a Bias. If the area of the smaller triangle is less than the area of the larger triangle divided by the bias, the triangles are swapped. This is useful for optimizing the triangulation of surveys such as SHOALS surveys.
- Contour Optimization – Triangle edges are swapped to minimize sharp angles in scalar contours and define localized topographical features more naturally.
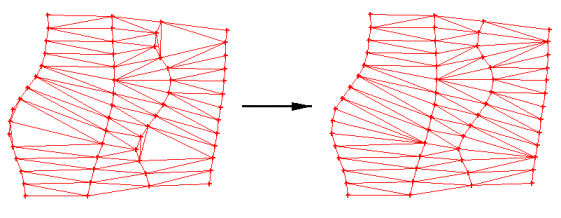
TIN Contour Optimization
Description It is known that a global optimum triangle configuration exists for any given set of scatter points. The qualitative accuracy of that global optimum will vary depending on the density of the available data. Despite its existence, there is no guarantee that a progressive edge-swap process, such as the one used by the contour optimization option, will converge to that global optimum. The likelihood that a global optimum will result varies inversely with the size of the data set. The contour smoothing algorithm will assuredly converge to a sub-optimum configuration and the smaller the data set, the more closely the result with approximate the global optimum. As demonstrated by this relationship, the contour smoothing algorithm works very well for discovering local optimums. Usage Guidelines The following are recommended guidelines for getting the most efficacy out of the contour optimization option.
Break down large data sets into smaller areas for optimization by selecting an area with the triangle selection tool before optimizing. This also has the benefit of decreasing the optimization runtime for the entire data set. Recognize that the more edges a contour deviation spans, the less likely it is that the optimization will correct the problem. It is recommended that large deviations, such as can be easily identified by the user, be minimized by the insertion of appropriately forced breaklines prior to optimization. A better optimization can be obtained for large datasets if locally selected optimization areas are chosen so as to overlap each other. This progressive edge-swap optimization is sensitive to initial conditions. Often by varying the initial triangulation (Delaunay, Area Bias or hybrid of both) a better optimization can be achieved.
By following these guidelines, the time spent identifying minor changes and swapping edges individually is greatly minimized. Please note that this optimization is iterative and larger data selections will not only require longer runtime but are also more likely to converge to any number of sub-optima dependent on the specific configuration of the triangles. This recommended process of user guided optimization is likely to require some repetition but proves to be much more time efficient for the user.
The following are some of the scenarios under which contour optimization is especially useful.
- Smoothing of channel banks.
- Refining topographical transitions between flat and steep areas.
- Streamlining jagged contours and contour jumps caused by triangulation.
- Connecting thalweg points between cross-sections.
In addition, the following are known limitations of the contour smoothing algorithm.
- Will not define small dams in narrow channels because of the indeterminate nature of the scatter point data.
- Large contour discontinuities and displacements that require the swapping of many edges in a sequential manner, without decreasing the departure angle, before achieving an optimum configuration are unlikely to resolve themselves using this method. It is recommended that the user insert breaklines to connect the proper points and force them prior to optimizing the area.
- Channel cross-sections that are inset into higher resolution scatter sets will result in unacceptable triangulation along the banks if triangulated together. It is recommended that the user either triangulate and optimize the cross-section scatter set separately and then merge the two together while preserving the cross-section set’s triangulation or, add and force breaklines connecting the endpoints of the cross-sections to better approximate the optimum before attempting to optimize.
- Users should be aware that large datasets, if optimized in their entirety, are likely to take excessive amounts of time to run. It is recommended that the user manually select smaller areas of large data sets to run incrementally and work through the data set in this manner. This method of user guided optimization drastically decreases the runtime required to optimize large data sets and allows the user to bypass any areas they believe to have acceptable triangulation.
Duplicate Vertex Options
When the Select/Delete Duplicate Points menu item is selected, points within a tolerance of other points are selected or deleted. The user sets the Tolerance and whether to delete or select the points when the command is invoked.
Related Topics
SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||