GMS:Subset Definition
In the IDW Interpolation Options dialog, an option is available for using a subset of the scatter points (as opposed to all of the available scatter points) in the computation of the nodal function coefficients and in the computation of the interpolation weights. Using a subset of the scatter points drops distant points from consideration since they are unlikely to have a large influence on the nodal function or on the interpolation weights. In addition, using a subset can speed up the computations since less points are involved.
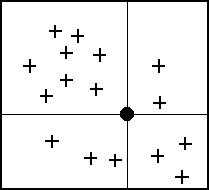
If the Use subset of points option is chosen, the Subsets button can be used to bring up the Subset Definition dialog. Two options are available for defining which points are included in the subset. In one case, only the nearest N points are used. In the other case, only the nearest N points in each quadrant are used as shown below. This approach may give better results if the scatter points tend to be clustered.
The Four Quadrants Surrounding an Interpolation Point.
If a subset of the scatter point set is being used for interpolation, a scheme must be used to find the nearest N points. Two methods for finding a subset are provided in the Subset Definition dialog: the global method and the local method.
Global Method
With the global method, each of the scatter points in the set are searched for each interpolation point to determine which N points are nearest the interpolation point. This technique is fast for small scatter point sets but may be slow for large sets.
Local Method
With the local methods, the scatter points are triangulated to form a temporary TIN before the interpolation process begins. To compute the nearest N points, the triangle containing the interpolation point is found and the triangle topology is then used to sweep out from the interpolation point in a systematic fashion until the N nearest points are found. The local scheme is typically much faster than the global scheme for large scatter point sets.
GMS – Groundwater Modeling System | ||
|---|---|---|
| Modules: | 2D Grid • 2D Mesh • 2D Scatter Point • 3D Grid • 3D Mesh • 3D Scatter Point • Boreholes • GIS • Map • Solid • TINs • UGrids | |
| Models: | FEFLOW • FEMWATER • HydroGeoSphere • MODAEM • MODFLOW • MODPATH • mod-PATH3DU • MT3DMS • MT3D-USGS • PEST • PHT3D • RT3D • SEAM3D • SEAWAT • SEEP2D • T-PROGS • ZONEBUDGET | |
| Aquaveo | ||