SMS:Laplacian Interpolation: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{SMS Deprecated Feature}} | |||
Laplacian interpolation is an interpolation/extrapolation approach that tries to give smooth gradients between areas of known values. Laplacian interpolation can only be performed on a cell-centered Cartesian grid. | Laplacian interpolation is an interpolation/extrapolation approach that tries to give smooth gradients between areas of known values. Laplacian interpolation can only be performed on a cell-centered Cartesian grid. | ||
When performing Laplacian interpolation, the values at each scatter vertex are considered known values and assigned to the Cartesian grid cells that they lie within. We will refer to the known locations/values as seed location/values. The seed values are held constant throughout the process. The algorithm assigns the average seed value to every cell in the grid. Once the initial values have been set, the algorithm repeatedly sweeps the grid smoothing the data values. The result gives the seed values at each of their locations and smooth transitions between the values. The algorithm will also extrapolate outside of the original seed values. | When performing Laplacian interpolation, the values at each scatter vertex are considered known values and assigned to the Cartesian grid cells that they lie within. We will refer to the known locations/values as seed location/values. The seed values are held constant throughout the process. The algorithm assigns the average seed value to every cell in the grid. Once the initial values have been set, the algorithm repeatedly sweeps the grid smoothing the data values. The result gives the seed values at each of their locations and smooth transitions between the values. The algorithm will also extrapolate outside of the original seed values. | ||
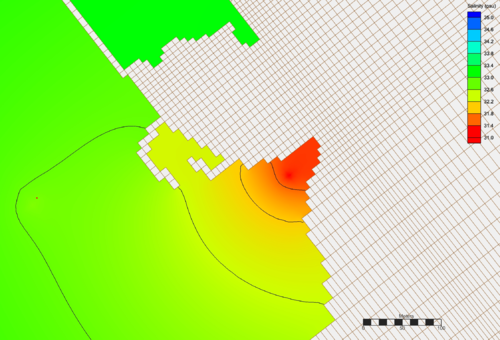
For models that distinguish between wet and dry cells (like CMS-Flow), the Laplacian interpolation will only be performed inside of wet (computational) cells. This gives the often desirable effect that the gradients will follow flow-paths. Cells that are nearby but do not have a water connection, will have a greater difference in value than cells that have a water connection. This effect can be seen in the image below. | For models that distinguish between wet and dry cells (like [[SMS:CMS-Flow|CMS-Flow]]), the Laplacian interpolation will only be performed inside of wet (computational) cells. This gives the often desirable effect that the gradients will follow flow-paths. Cells that are nearby but do not have a water connection, will have a greater difference in value than cells that have a water connection. This effect can be seen in the image below. | ||
[[File:LaplacianInterpolation zoomed in.png|thumb|none|left|500 px|Laplacian interpolation for salinity values]] | :[[File:LaplacianInterpolation zoomed in.png|thumb|none|left|500 px|Laplacian interpolation for salinity values]] | ||
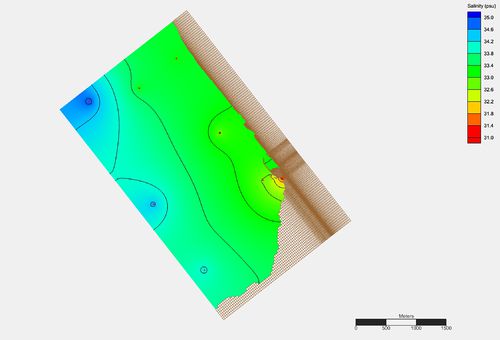
The picture below is of the same domain but zoomed out so the full domain can be shown. Notice the smooth transitions between distinct values. | The picture below is of the same domain but zoomed out so the full domain can be shown. Notice the smooth transitions between distinct values. | ||
[[File:LaplacianInterp.jpg|thumb|none|left|500 px|Laplacian interpolation for salinity full domain]] | :[[File:LaplacianInterp.jpg|thumb|none|left|500 px|Laplacian interpolation for salinity full domain]] | ||
| Line 15: | Line 16: | ||
[[Category:SMS Interpolation|L]] | [[Category:SMS Interpolation|L]] | ||
[[Category:Archived]] | |||
Latest revision as of 21:52, 19 November 2018
| This contains information about features no longer in use for the current release of SMS. The content may not apply to current versions. |
Laplacian interpolation is an interpolation/extrapolation approach that tries to give smooth gradients between areas of known values. Laplacian interpolation can only be performed on a cell-centered Cartesian grid.
When performing Laplacian interpolation, the values at each scatter vertex are considered known values and assigned to the Cartesian grid cells that they lie within. We will refer to the known locations/values as seed location/values. The seed values are held constant throughout the process. The algorithm assigns the average seed value to every cell in the grid. Once the initial values have been set, the algorithm repeatedly sweeps the grid smoothing the data values. The result gives the seed values at each of their locations and smooth transitions between the values. The algorithm will also extrapolate outside of the original seed values.
For models that distinguish between wet and dry cells (like CMS-Flow), the Laplacian interpolation will only be performed inside of wet (computational) cells. This gives the often desirable effect that the gradients will follow flow-paths. Cells that are nearby but do not have a water connection, will have a greater difference in value than cells that have a water connection. This effect can be seen in the image below.
The picture below is of the same domain but zoomed out so the full domain can be shown. Notice the smooth transitions between distinct values.
SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||