GMS:TIN Display Options: Difference between revisions

From XMS Wiki
Jump to navigationJump to search
No edit summary
No edit summary
Line 26: Line 26:
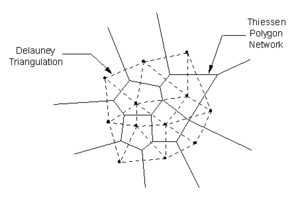
| Thiessen polygons || If the ''Thiessen polygons'' item is set, a Thiessen polygon for each TIN vertex is displayed each time the display is refreshed. The edges of the Thiessen polygons are formed by the perpendicular bisectors of the edges of the triangles in the TIN. The vertices of these polygons correspond to the centers of the circumcircles of the [[GMS:Triangulation|Delaunay triangulation]]. Any location inside a Thiessen polygon is closer to the TIN vertex contained in that polygon than to any other TIN vertex. The red polygons in the image below correspond to the Thiessen polygons for this TIN.
| Thiessen polygons || If the ''Thiessen polygons'' item is set, a Thiessen polygon for each TIN vertex is displayed each time the display is refreshed. The edges of the Thiessen polygons are formed by the perpendicular bisectors of the edges of the triangles in the TIN. The vertices of these polygons correspond to the centers of the circumcircles of the [[GMS:Triangulation|Delaunay triangulation]]. Any location inside a Thiessen polygon is closer to the TIN vertex contained in that polygon than to any other TIN vertex. The red polygons in the image below correspond to the Thiessen polygons for this TIN.


: [[Image:thiessen.png|thumb|none|200px]]
: [[Image:thiessen.png|thumb|none|300px]]
|-
|-
| Circumcircles || If the ''Circumcircles'' item is set, the circumcircle enclosing the three vertices for each triangle are drawn when the display is refreshed. Circumcircles provide the basis of a [[GMS:Triangulation|Delaunay triangulation]] since the Delaunay criterion is satisfied by ensuring that no circumcircle encloses a vertex. Displaying circumcircles can aid in the understanding of the triangulation process. The red circles in the figure are the circumcircles for the TIN.
| Circumcircles || If the ''Circumcircles'' item is set, the circumcircle enclosing the three vertices for each triangle are drawn when the display is refreshed. Circumcircles provide the basis of a [[GMS:Triangulation|Delaunay triangulation]] since the Delaunay criterion is satisfied by ensuring that no circumcircle encloses a vertex. Displaying circumcircles can aid in the understanding of the triangulation process. The red circles in the figure are the circumcircles for the TIN.

Revision as of 15:06, 19 April 2016

TIN Module
Tins.png
TINs
Creating a TIN
Editing a TIN
Converting TINS to Other Data Types
Building Solids and 3D Meshes with TINs
Map to MODFLOW with TINs
More
TIN Settings
TIN Display Options
TIN Tool Palette
TIN Commands
TIN Files
v • e

The properties of all TIN data that GMS displays on the screen can be controlled through the TIN tab of the Display Options dialog. This dialog is opened by right-clicking on the File:TINFolder.GIF TIN Data entry in the Project Explorer and selecting the Display Options command. It can also be accessed from the from the Display menu or the Display Options macro.png The following table describes the display options available for the TIN module.

Display Option Description
Vertices If the Vertices item in the TIN Display Options dialog is set, the TIN vertices are displayed each time the Graphics Window is refreshed. Since it is possible to accidentally drag points, vertices can be "locked" to prevent them from being dragged or edited by selecting the Lock ALL Vertices command from the TINs menu. Vertices can be unlocked by unchecking the Lock ALL Vertices command in the TINs menu. Both a "Locked" and "Unlocked" vertex color may be set so that there is a visible difference when displaying the TIN. (See Editing TINs)
Triangle edges If this item is on the lines that make up each triangle are displayed. The color of the triangle edges can be adjusted according to the following options:
  1. Auto – draws the material color if faces are not displayed. Uses black or white if the faces are displayed.
  2. Specified – used the color specified next to the triangle edges
  3. Material – displays the material color of the triangle
Triangle faces The Triangle faces item causes the faces of the triangles to be drawn as filled polygons.
Texture map image to active TIN The Texture map image item is used to "drape" an image over the surface of the TIN.
TIN boundary The TIN boundary feature is often used in conjunction with contours in order to display the contours without cluttering the screen by displaying each triangle. The first image below shows contours displayed together with the TIN triangles. The second image shows contours displayed with the TIN boundary.
File:Contour w tri.gif
File:Contour wo tri.gif
Thiessen polygons If the Thiessen polygons item is set, a Thiessen polygon for each TIN vertex is displayed each time the display is refreshed. The edges of the Thiessen polygons are formed by the perpendicular bisectors of the edges of the triangles in the TIN. The vertices of these polygons correspond to the centers of the circumcircles of the Delaunay triangulation. Any location inside a Thiessen polygon is closer to the TIN vertex contained in that polygon than to any other TIN vertex. The red polygons in the image below correspond to the Thiessen polygons for this TIN.
Thiessen.png
Circumcircles If the Circumcircles item is set, the circumcircle enclosing the three vertices for each triangle are drawn when the display is refreshed. Circumcircles provide the basis of a Delaunay triangulation since the Delaunay criterion is satisfied by ensuring that no circumcircle encloses a vertex. Displaying circumcircles can aid in the understanding of the triangulation process. The red circles in the figure are the circumcircles for the TIN.
File:Circum.gif
Vertex numbers If the Vertex numbers item is set, the number of each vertex is displayed adjacent to the vertex.
Scalar values If the Scalar values item is set, the active dataset value of each vertex is displayed adjacent to the vertex.
Contours Most of the objects supported by GMS can be contoured by turning on the Contour Options in the Display Options dialog. When an object is contoured, the values associated with the active dataset for the object are used to generate the contours.
Vectors If the Vectors item in the Display Options dialog is selected for an object (TIN, Grid, or Mesh), vector plots can be generated using the active vector dataset for the object. One vector is placed at each node, cell, or vertex.
File:DisplayTIN.jpg
The Display Options dialog showing the TIN tab.


v • e
GMS – Groundwater Modeling System
Modules:2D Grid  •  2D Mesh  •  2D Scatter Point  •  3D Grid  •  3D Mesh  •  3D Scatter Point  •  Boreholes  •  GIS  •  Map  •  Solid  •  TINs  •  UGridsGMS Logo2.png
Models:FEFLOW  •  FEMWATER  •  HydroGeoSphere  •   MODAEM  •  MODFLOW  •  MODPATH  •  mod-PATH3DU  •  MT3DMS  •  MT3D-USGS  •  PEST  •  PHT3D  •  RT3D  •  SEAM3D  •  SEAWAT  •  SEEP2D  •  T-PROGS  •  ZONEBUDGET
Aquaveo
Retrieved from "https://www.xmswiki.com/index.php?title=GMS:TIN_Display_Options&oldid=103553"