SMS:Linear Interpolation
If the linear interpolation scheme is selected, the 2D scatter points are first triangulated to form a temporary TIN. If the surface is assumed to vary linearly across each triangle, the TIN describes a piecewise linear surface which interpolates the scatter points. The equation of the plane defined by the three vertices of a triangle is as follows:
- where A, B, and C>, and D are computed from the coordinates of the three vertices (x1,y1,z1), (x2,y2,z2), and (x3,y3,z3):
The plane equation can also be written as:
- which is the form of the plane equation used to compute the elevation at any point on the triangle.
Since a TIN only covers the convex hull of a scatter point set, extrapolation beyond the convex hull is not possible with the linear interpolation scheme. Any points outside the convex hull of the scatter point set are assigned the default extrapolation value entered at the bottom of the Interpolation Options dialog.
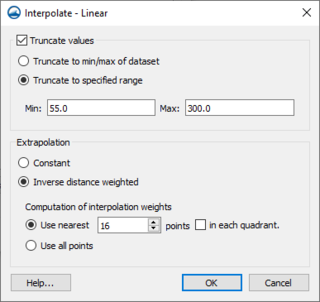
Interpolate Linear Dialog
The Interpolate – Linear dialog is reached from the Interpolation Options dialog. It contains the following options:
- Truncate values – This section allows for limiting the interpolated values to lie between the minimum and maximum value.
- Truncate to min/max of dataset – Limits the interpolated values to the minimum and maximum values in the original dataset.
- truncate to specified range – Allows setting a user specified minimum and maximum value range.
- Min – Manually sets a minimum value.
- Max – Manually sets a maximum value.
- Extrapolation
- Constant
- Value
- Inverse distance weighted
- Computation of interpolation weights
- Use nearest
- Use all points
- Constant
Related Topics
| [hide] SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||