GMS:Strike Dip Markov Chain: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
|||
| Line 13: | Line 13: | ||
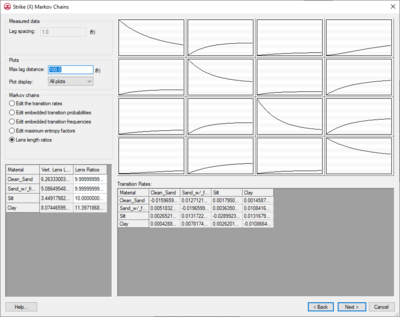
Typical site stratigraphic data is conducive to developing vertical spatial variability. However, rarely is the quantity of data adequate to develop an accurate model in the lateral directions. The combination of Walther’s Law and the transition probability approach allows for a logical method of developing lateral spatial variability from vertical spatial variability. Walther’s Law states that vertical successions of deposited facies represent the lateral succession of environments of deposition. Therefore, a logical method of generating a 3-D model of spatial variability would be first to develop a 1-D Markov chain in the [[GMS:Vertical Markov Chain|vertical direction]] based on site data, assuming there is such data. Second, using Walther’s Law and geologic knowledge, one can develop lateral, strike and dip, Markov chains of spatial variability. However, one issue that arises when applying vertical transition trends to lateral directions is how to cope with asymmetric vertical trends like fining upwards. For example, if in the vertical direction, sand tends to deposit on gravel as would be typical in a fluvial deposition, there will be a transition rate associated with the transition of "sand->gravel" and "gravel->sand". The transition of "gravel->sand" will be greater than "sand->gravel" because of the fining upward trend. However, in the lateral direction, which of these transition rates should be applied? Although the trend of sand next to gravel remains in the lateral direction, the transition rates of "sand->gravel" and "gravel->sand" should be equivalent or symmetric as defined by | Typical site stratigraphic data is conducive to developing vertical spatial variability. However, rarely is the quantity of data adequate to develop an accurate model in the lateral directions. The combination of Walther’s Law and the transition probability approach allows for a logical method of developing lateral spatial variability from vertical spatial variability. Walther’s Law states that vertical successions of deposited facies represent the lateral succession of environments of deposition. Therefore, a logical method of generating a 3-D model of spatial variability would be first to develop a 1-D Markov chain in the [[GMS:Vertical Markov Chain|vertical direction]] based on site data, assuming there is such data. Second, using Walther’s Law and geologic knowledge, one can develop lateral, strike and dip, Markov chains of spatial variability. However, one issue that arises when applying vertical transition trends to lateral directions is how to cope with asymmetric vertical trends like fining upwards. For example, if in the vertical direction, sand tends to deposit on gravel as would be typical in a fluvial deposition, there will be a transition rate associated with the transition of "sand->gravel" and "gravel->sand". The transition of "gravel->sand" will be greater than "sand->gravel" because of the fining upward trend. However, in the lateral direction, which of these transition rates should be applied? Although the trend of sand next to gravel remains in the lateral direction, the transition rates of "sand->gravel" and "gravel->sand" should be equivalent or symmetric as defined by | ||
<!--[[Image:t-progs_eq4.png]] | <!--[[Image:t-progs_eq4.png]] | ||
<math>r_{jk}=\frac{p_k}{p_j}r_{kj}</math> | <math>r_{jk}=\frac{p_k}{p_j}r_{kj}</math>--> | ||
[[Image:strikedipchain1.jpg]] | |||
The strategy for averaging the vertical transition rates to come up with the lateral rates is given in the three steps below. | The strategy for averaging the vertical transition rates to come up with the lateral rates is given in the three steps below. | ||