GMS:Vertical Markov Chain: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
|||
| Line 29: | Line 29: | ||
|page=6 | |page=6 | ||
}}</ref></div> | }}</ref></div> | ||
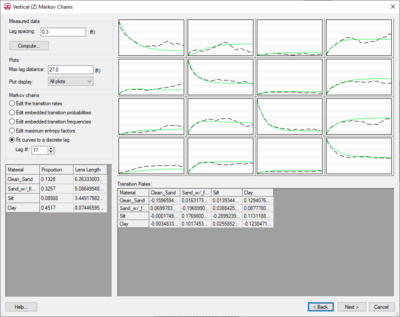
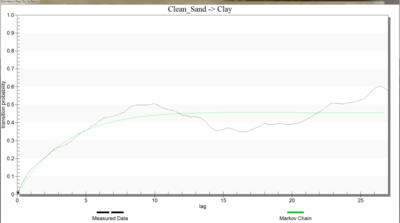
where x is a spatial location, h is the lag (separation vector), and j,k denote materials. The lag is defined by the Lag spacing item in the upper left corner of the Vertical (Z) Markov Chains dialog. The curve shown with the solid line is called a “Markov Chain”. The Markov Chains are used to formulate the equations used by T-PROGS to generate the multiple material sets during the simulation stage. The objective of this stage of the analysis is to fit the Markov Chain curves as accurately as possible to the measured transition probability curves. This process is similar to fitting a model variogram to an experimental variogram in a kriging exercise. The transition rates are adjusted to ensure a good fit between the Markov Chain model and the observed transition probability data. | where x is a spatial location, h is the lag (separation vector), and j,k denote materials. The lag is defined by the Lag spacing item in the upper left corner of the ''Vertical (Z) Markov Chains'' dialog. The curve shown with the solid line is called a “Markov Chain”. The Markov Chains are used to formulate the equations used by T-PROGS to generate the multiple material sets during the simulation stage. The objective of this stage of the analysis is to fit the Markov Chain curves as accurately as possible to the measured transition probability curves. This process is similar to fitting a model variogram to an experimental variogram in a kriging exercise. The transition rates are adjusted to ensure a good fit between the Markov Chain model and the observed transition probability data. | ||
It should be noted that the self-transitional curves on the diagonal start at a probability of 1.0 and decrease with distance and the off-diagonal curves start at zero probability and increase with distance. In both cases, the curves eventually flatten out at some distance. The probability corresponding to the flat part of the curve represents the mean proportion of the material. All curves on a particular column should flatten out to the same proportion. The proportions are displayed in the lower left corner of the dialog. The point where a tangent line from the early part of the curves on the diagonal intersects the horizontal (lag distance) axis on each curve represents the mean lens length for the material. The mean lens lengths are shown just to the right of the mean proportions in the lower left part of the dialog. The slope at the beginning of each of the Markov Chains represents the transition rate. Together, the proportions, lens lengths, and transition rates define the Markov Chains. | It should be noted that the self-transitional curves on the diagonal start at a probability of 1.0 and decrease with distance and the off-diagonal curves start at zero probability and increase with distance. In both cases, the curves eventually flatten out at some distance. The probability corresponding to the flat part of the curve represents the mean proportion of the material. All curves on a particular column should flatten out to the same proportion. The proportions are displayed in the lower left corner of the dialog. The point where a tangent line from the early part of the curves on the diagonal intersects the horizontal (lag distance) axis on each curve represents the mean lens length for the material. The mean lens lengths are shown just to the right of the mean proportions in the lower left part of the dialog. The slope at the beginning of each of the Markov Chains represents the transition rate. Together, the proportions, lens lengths, and transition rates define the Markov Chains. | ||
Several methods are provided for fitting the Markov Chains to the measured transition probability curves. These methods are listed in the section of the dialog titled | Several methods are provided for fitting the Markov Chains to the measured transition probability curves. These methods are listed in the section of the dialog titled ''Markov Chains''. By default, GMS automatically makes an attempt to fit the curves using the '''Edit maximum entropy factors''' option. In many cases, this fit is sufficiently accurate and we can proceed to the next step. However, it is often useful to explore the other options for fitting the curves. | ||
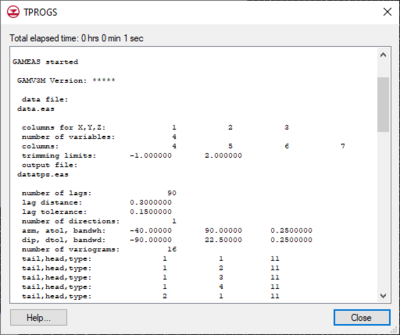
If boreholes exist in the model, the | If boreholes exist in the model, the '''Compute...''' button becomes undimmed. When the user clicks the '''Compute...''' button, the parameter files required for running GAMEAS are generated and GAMEAS is executed. | ||
===GAMEAS=== | ===GAMEAS=== | ||
| Line 41: | Line 41: | ||
GAMEAS is an algorithm that processes borehole data and determines geologic characteristics such as material proportions and transition probability curves in a given direction. A separate window displays the details of the GAMEAS run, which allows the user to monitor the output from the GAMEAS simulation. | GAMEAS is an algorithm that processes borehole data and determines geologic characteristics such as material proportions and transition probability curves in a given direction. A separate window displays the details of the GAMEAS run, which allows the user to monitor the output from the GAMEAS simulation. | ||
When GAMEAS completes a successful run, the results, including the material proportions and transition probability curves from the measured data, are read into the corresponding data fields in the | When GAMEAS completes a successful run, the results, including the material proportions and transition probability curves from the measured data, are read into the corresponding data fields in the ''Vertical Markov Chain'' dialog. Furthermore, the transition rates which correspond to the slope of the transition probability curves when the lag equals 0 are interpolated from the measured data curves. In addition to running GAMEAS, the code parses through the borehole data and calculates the embedded transition probabilities and frequencies. These values are stored in arrays that correspond to options #2 and #3 in the Markov Chains section of the dialog. | ||
===Lag=== | ===Lag=== | ||
| Line 48: | Line 48: | ||
==Markov chains section== | ==Markov chains section== | ||
There are five alternate methods of generating Markov chains in this section (area in the | There are five alternate methods of generating Markov chains in this section (area in the ''Vertical Markov Chain'' dialog). These methods are in a radio-button configuration to allow the user to conveniently change from one method to another. Each of these five methods will be described. | ||
*[[#Edit the transition rates|Edit the transition rates]] | *[[#Edit the transition rates|Edit the transition rates]] | ||
| Line 89: | Line 89: | ||
=== Fit curves to a discrete lag === | === Fit curves to a discrete lag === | ||
This option is only undimmed if a transition probability curve from measured data exists in memory. When this option is selected, the Lag # edit field is undimmed and the user enters the discrete lag the curves will be fit to. | This option is only undimmed if a transition probability curve from measured data exists in memory. When this option is selected, the '''Lag #''' edit field is undimmed and the user enters the discrete lag the curves will be fit to. | ||
This option produces Markov chains that are computed from the measured transition rates produced by GAMEAS. GAMEAS computes a set of transition probabilities at each lag specified by the user. This option computes an array of transition rates from the slope of the curves generated by GAMEAS (green). The transition rates correlate to the shape of the curve from the origin to the lag # specified by the user in the Lag # edit field. Therefore, the cells of all the spreadsheets in the dialog are dimmed because the values are inherited from the measured curves (green). The values in the spreadsheets change depending on the lag # entered. By adjusting the lag interval, an excellent fit can often be obtained. | This option produces Markov chains that are computed from the measured transition rates produced by GAMEAS. GAMEAS computes a set of transition probabilities at each lag specified by the user. This option computes an array of transition rates from the slope of the curves generated by GAMEAS (green). The transition rates correlate to the shape of the curve from the origin to the lag # specified by the user in the Lag # edit field. Therefore, the cells of all the spreadsheets in the dialog are dimmed because the values are inherited from the measured curves (green). The values in the spreadsheets change depending on the lag # entered. By adjusting the lag interval, an excellent fit can often be obtained. | ||