SMS:CGWAVE: Difference between revisions
(→External Links:: Updated link to better version of the PDF and reduced info to just the titles) |
(→Boundary Conditions: Clarified convergence tolerance purpose) |
||
| Line 72: | Line 72: | ||
=== Boundary Conditions === | === Boundary Conditions === | ||
The input wave condition (amplitude, period, direction) must be specified at the end of the 1-d cross-section. | The input wave condition (amplitude, period, direction) must be specified at the end of the 1-d cross-section. Simulations are less reliable (not necessarily wrong) if the waves approach the coast at a glancing angle (say within 20° of the coastline). The 1-d sections MUST reach out further than the outermost point of the semicircle. The domain should have no zero or negative depths; the land-water interface must be demarcated using a small water depth (say 0.5 m, but the limit depends on the overall water depths and wave periods and the problem being solved). Note that making this too shallow may result in a large number of grids in this area which may not be necessary for all applications). | ||
For basic specifications, the incident wave angle specification is as follows. Waves going in the +x axis (i.e. to East) are specified as incident angle =0°. Waves going in +y direction (i.e. to North) are specified as incident angle =90°, to West =180°, to South = 270° . Incident wave direction is used in degrees. Convergence tolerance is typically assigned 10<sup>-8</sup>, output frequency is 100 every iterations. | For basic specifications, the incident wave angle specification is as follows. Waves going in the +x axis (i.e. to East) are specified as incident angle =0°. Waves going in +y direction (i.e. to North) are specified as incident angle =90°, to West =180°, to South = 270° . Incident wave direction is used in degrees. Convergence tolerance is typically assigned 10<sup>-8</sup>, output frequency is 100 every iterations. When error values come within the set convergence tolerance CGWAVE will cease running iterations. | ||
For the boundary condition specification, the ''parabolic plus two 1d sections'' option (Option 3 in *.cgi) should be chosen for most harbor problems, with a semicircle open boundary; in earlier versions, it is possible to use the option with just one 1d section (Option 2 in *.cgi) but it really provides no benefit over Option 3. | For the boundary condition specification, the ''parabolic plus two 1d sections'' option (Option 3 in *.cgi) should be chosen for most harbor problems, with a semicircle open boundary; in earlier versions, it is possible to use the option with just one 1d section (Option 2 in *.cgi) but it really provides no benefit over Option 3. The other options consist of the ''parabolic approximation'' (Option 1 in *.cgi) which is suitable if the exterior region is of constant depth. The ''Fourier Bessel Series'' (Option 0 in *.cgi) must be used if its limitations, described above in Section 2.2 (equations 15-17), are met; typically it is sufficient to specify 15 terms in the infinite series. For harbor problems, SMS will create the 1d sections based on depths based on depths on semicircle, and the desired grid spacing (used to solve the 1d equation (20)), based on (approximately) L/10 must be specified in the dialog box: | ||
Revision as of 21:54, 1 December 2016
| CGWAVE | |
|---|---|
| Model Info | |
| Model type | General-purpose wave prediction model for simulating the propagation and transformation of ocean waves in coastal regions and harbors, and appropriate for modeling the most significant physical processes in channels, inlets and harbors, open coastal regions, around islands and structures. |
| Developer | Zeki Demirbilek, Ph.D. |
| Web site | CGWAVE web site |
| Tutorials |
General Section
Models Section
Several sets of sample problems and case studies are available. These include:
|
The model CGWAVE (Demirbilek and Panchang 1998) is a two-dimensional wave transformation model that can be used to predict wave properties (wave heights, velocities, pressures, radiation stresses) in domains of complex shape and depth variations when an input wave condition (amplitude, direction, and period; or a spectral combination of these) is provided.
The CGWAVE model can be added to a paid edition of SMS.
Graphical Interface
SMS provides a graphical interface that is designed to to visualize the projects being created, easily modify project parameters, and view the solutions produced by the CGWAVE model.
The CGWAVE Graphical Interface contains tools to create and edit an CGWAVE simulation. The simulation consists of a geometric definition of the model domain (the mesh) and a set of numerical parameters. The parameters define the boundary conditions and options pertinent to the model.
The interface is accessed by selecting the 2D Mesh Module and setting the current model to CGWAVE. If a mesh has already been created for a CGWAVE simulation or an existing simulation read, the mesh object will exist in the Project Explorer and selecting that object will make the 2D Mesh module active and set the model to CGWAVE. See Building a Mesh for more information.
The interface consists of the 2D Mesh Module Menus and tools augmented by the CGWAVE menu. See CGWAVE Graphical Interface for more information.
Functionality
The model is based on extensions of the “combined refraction-diffraction” equation, which is applicable to both long and short waves and hence finds wide application in coastal engineering and harbor resonance studies. Being elliptic, the equation represents a boundary value problem, which can accommodate internal non-homogeneities (islands, structures, etc.) and boundaries. It hence forms a well-accepted basis for performing wave simulations in regions with arbitrarily-shaped (manmade or natural) boundaries and arbitrary depth variations without limitations on the angle of wave incidence or the degree and direction of wave reflection and scattering that can be modelled. In essence, it represents the complete two-dimensional wave-scattering problem for the non-homogeneous Helmholtz equation. Irregular wave conditions may be simulated using (1) by superposition of monochromatic simulations (e.g. Chawla et al. 1998; Panchang et al. 1990; Zhao et al. 2001.)
The wave phenomena that can be simulated with CGWAVE are: bathymetric refraction, diffraction by structures (e.g. breakwaters) and the bathymetry, reflection (from structures and natural boundaries (seawalls, coastlines, etc) as well as from bed slopes), friction, breaking, and floating (fixed) docks. The model uses a triangular finite-element formulation with grid sizes varying throughout the domain based on the local wavelength; the grids can be efficiently generated using the SMS graphical interface when a bathymetry file is provided. The model allows one to specify the desired reflection properties along the coastline and other internal boundaries. It is therefore particularly well-suited for simulating waves in harbors. While the basic equation is intended for monochromatic waves, irregular (i.e. spectral) wave conditions are simulated in CGWAVE through a linear superposition of monochromatic simulations (e.g. Panchang et al. 1990; Zhao et al. 2001.) Typically, simulations involving a domain containing hundreds of thousands of finite element nodes can be performed in a few minutes on a PC.
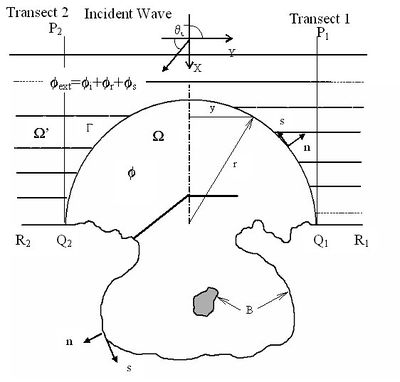
For harbor applications, the model also uses a semi-circle (as an open boundary) to separate the model domain from the outer sea. A typical CGWAVE model domain is shown in Fig. 1. The input conditions are provided at the offshore ends of two one-dimensional cross-shore sections. (In practice, the input condition is known at the end of one of the transects. The condition at the offshore end of the other transect is obtained by appropriate phase translation.) A combination of the incident and reflected waves is computed along these transects using a one-dimensional version of the governing equation; this partial solution is then mapped on to the semicircle to force the two-dimensional model. The remainder of the solution on the boundary consists of a scattered wave that emanates from within the domain; this component is allowed to radiate out through the use of an impedance boundary condition. In the model interior, a finite-element grid is used to represent the depth field, and the coastlines (denoted by B in Fig. 1) are assigned a reflection coefficient. For open ocean applications, all variations must be included inside a circle, outside which the depths are assumed constant (Panchang et al. 2000).
Functionalities
- CGWAVE Flies
- CGWAVE Graphical Interface
- CGWAVE Model Checker
- CGWAVE Model Control
- Saving CGWAVE files
Using the Model / Practical Notes
Methodology
When beginning a new project, first a domain must be created to perform the calculations. This domain comes from a combination of the coastline (land side of the domain) and the bathymetric survey. Begin by reading the survey into SMS and making sure it is an adequate and accurate representation of the study area. Ensure that the data covers the entire domain, and that the existing (or natural) coastline is adequately defined. If the survey includes topographic data, the coastline can be extracted as a contour of constant depth. Since CGWAVE does not support calculation of wave run-up, this should always be a positive depth (0.5 m or so is recommended). Follow the mesh generating techniques demonstrated in the tutorial problem for CGWAVE.
After creating the finite element mesh, it may be useful to make an initial run of CGWAVE in linear mode with fully absorbing coastlines and an incident wave condition. If desired, include both a normally incident wave run, and a separate obliquely incident wave. When CGWAVE is run in linear mode, the solution is unlimited and technically wave heights coming from the solution can grow uncontrolled. Numerically, there is no limit on wave heights. This is not realistic since waves in nature are finite in height (wave heights are depth-limited in shallow-water depths). However, the resulting solutions, especially the phase diagrams, can be used to perform visual quality control, since forward propagating waves are the easiest for making intuitive assessments (e.g. spacing between crests should be smaller and wave heights generally increasing in shallower water; bending of phase-lines for oblique incidence to approach the shore in a normal fashion, high wave heights in very shallow water because breaking was not applied, etc).
Repeating the incident runs with full reflection should lead to some standing wave patterns (large and small wave heights; rapid change of phase). A visual examination of the results will enhance confidence in later simulations.
Domain Shape
A mesh for use with CGWAVE must match one of two domain shapes. For cases involving a continuous coastline, the ocean boundary should be semi-circular. For cases examining waves around an island, the domain should be circular. The interface includes tools to build rectangular domains along coastlines, however, this is for research purposes only and should not be applied in projects with the current versions of CGWAVE. SMS includes tools in the Map Module to create a network with a valid domain shape (see the tutorial for CGWAVE). Therefore, it is strongly recommended that the Map Module be the principal method for creation of new networks. The Mesh Module may be used to create a mesh, however in the case of CGWAVE the Mesh Module primarily is useful for network editing and assigning model parameters required by CGWAVE. These model parameter commands are grouped in the CGWAVE menu.
To the extent possible, it is necessary to have the coastlines outside the semicircle be as straight as possible, and ideally, parallel to one of the axes (as shown in Fig 1). The semicircle should be so located that the depths outside vary, to the extent possible, in a 1-d (cross-shore) direction only in the exterior. These depths are introduced in the model through the two 1-d sections. It's necessary to specify a reflection coefficient for the exterior coastline.
Of course, these conditions are not encountered in practice in an ideal manner, but it is important to understand that the model works under these assumptions. V-shaped coastlines do not meet these criteria. Also, not all real domains have 1-dimensionally varying exterior depths. Regions with 2-d depth variations should preferably be incorporated inside the semicircle and it may be necessary to enlarge the domain so that solutions in the area of interest (hopefully) are not affected by the coastline shape. It is impossible to accommodate all real topographic variations of the model’s exterior domain. Since a part of what happens outside the semicircle influences the solution within (i.e. how the backscattered waves behave), some simplified representation of the exterior is needed. The exterior representation used in CGWAVE is more sophisticated than that used in earlier models (which assumed collinear and fully reflecting coastlines and constant exterior depths).
A full circle option is available for open sea problems where the exterior is of constant depth; the theoretical ideal for this is the Fourier Bessel Series (which works for unit wave input only); the parabolic mode may also be used (Panchang et al. 2000) with little loss of accuracy.
Domain Size
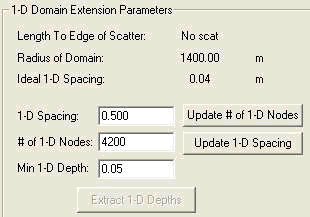
The size of the domain is also governed by the wavelength. Typically, the minimum radius for the semicircle should be about 2 or 3 times the wavelength, which also dictates the overall number of grids. It is important that the modeler first estimate the number of grid points needed, at least in an approximate sense. This can be done by estimating a nominal wavelength L (based on the period and depth), and using L/10 as a rough measure of the grid size. Obviously, large domains with short period waves will lead to hundreds of thousands of nodes. This is not a problem physically, but can be very time consuming to simulate. For spectral conditions, the domain size should be dictated by the longer wavelengths L1 (say radius = 3L1), but the resolution for the shorter wavelengths (L2) would be, say L2/10, which may be excessively fine for the longer wavelengths. Obviously, some care (and perhaps compromise) is needed in designing the grid and also selecting the input spectral components. If some components have little energy, it may be best to delete them from the modeling.
Boundary Conditions
The input wave condition (amplitude, period, direction) must be specified at the end of the 1-d cross-section. Simulations are less reliable (not necessarily wrong) if the waves approach the coast at a glancing angle (say within 20° of the coastline). The 1-d sections MUST reach out further than the outermost point of the semicircle. The domain should have no zero or negative depths; the land-water interface must be demarcated using a small water depth (say 0.5 m, but the limit depends on the overall water depths and wave periods and the problem being solved). Note that making this too shallow may result in a large number of grids in this area which may not be necessary for all applications).
For basic specifications, the incident wave angle specification is as follows. Waves going in the +x axis (i.e. to East) are specified as incident angle =0°. Waves going in +y direction (i.e. to North) are specified as incident angle =90°, to West =180°, to South = 270° . Incident wave direction is used in degrees. Convergence tolerance is typically assigned 10-8, output frequency is 100 every iterations. When error values come within the set convergence tolerance CGWAVE will cease running iterations.
For the boundary condition specification, the parabolic plus two 1d sections option (Option 3 in *.cgi) should be chosen for most harbor problems, with a semicircle open boundary; in earlier versions, it is possible to use the option with just one 1d section (Option 2 in *.cgi) but it really provides no benefit over Option 3. The other options consist of the parabolic approximation (Option 1 in *.cgi) which is suitable if the exterior region is of constant depth. The Fourier Bessel Series (Option 0 in *.cgi) must be used if its limitations, described above in Section 2.2 (equations 15-17), are met; typically it is sufficient to specify 15 terms in the infinite series. For harbor problems, SMS will create the 1d sections based on depths based on depths on semicircle, and the desired grid spacing (used to solve the 1d equation (20)), based on (approximately) L/10 must be specified in the dialog box:
Wave Breaking
There are two methods for applying wave breaking. For practical problems, it's recommended to make a non-breaking simulation and then applying an H/d limit (generally between 0.6 and 0.85) to alter the calculated wave heights to the limit (say 0.78d). The other, more rigorous approach is to run the model in the nonlinear breaking mode where breaking properties are continuously recalculated based on prior solutions. This requires several rounds of iterations and is recommended for special problems and/or research applications. For nonlinear runs, the maximum number of nonlinear iterations is generally specified as 15 with a tolerance of 10-6. For spectral simulations, obviously the former approach is recommended.
Docks
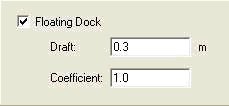
For incorporating docks, the actual “without-dock” water depth is originally specified while generating the grid; areas covering the docks must then be highlighted, and a draft and coefficient as shown in the dialog below.
The draft depth is a physical quantity and can be measured on an existing structure or designed. The coefficient, which is called alpha here, is a numerical term that impacts the conveyance of energy under the dock. It is a function of the wave number of the wave passing the dock (k), the characteristic structure size (a), the depth (h) and the draft (d) of the dock. A review of the theory can be found in Tsay and Liu (1983).
To compute an appropriate coefficient, the following process can be followed:
- Compute ka, kh and d/h
- Limit value of kh
- if (kh > 4) kh = 4
- if (kh < 0.1) kh = 0.1
- Compute initial value of alpha as:
- if (kh <= 2) alpha = 0.97 - (0.65*kh) + (0.1*kh*kh)
- if (kh > 2) alpha = 0.09 - 0.02*kh
- Adjust alpha for d/h
- alpha = alpha*(1.4-0.8*(d/h))
- Adjust alpha for ka
- if (ka < 1) alpha = 0.8*alpha
Visualizing Solutions
Solutions generated by CGWAVE can be visualized in SMS in two ways. The most straightforward method is to read the solution file. When SMS reads this solution file, it translates the data and creates datasets for wave amplitude, direction and phase. If additional functions are desired from the wave characteristics, they must be generated using a CGWAVE translating utility. An example of this is included in the CGWAVE reference manual. The translating utility creates generic dataset files that can be imported using the Data Browser.
Mesh Generation
CGWave computes properties that illustrate the characteristics of waves in a coastal area. To adequately perform this approximation, the mesh must contain several elements per wavelength. Steps for generating a mesh for CGWAVE are spelled out in the description of the Graphical Interface.
Saving CGWAVE
When completed a File | Save As... command, the following files get saved in the *.sms
- *.mat referenced to new save location
- *.map referenced to new save location
- *.cgi referenced to new save location
- *.h5 referenced to new save location
- *.cgo referenced to old save location unless rerun then referenced to new save location
What does the error message “Number of Nodes Exceeded the Dimension” mean?
This message indicates the mesh has more elements than the program is dimensioned for. Running with more nodes/elements than the program is dimensioned for is not recommended. CGWAVE can be compiled for larger dimensions if necessary for a specific case. Contact tech support for more information.
Memory Requirements and Notes
Currently the CGWAVE engine is written in FORTRAN. All memory management in the program is handled with static arrays. An effort is currently underway to rewrite the code to use dynamic arrays. The executable distributed with SMS has been compiled to handle meshes with up to approximately 480,000 nodes. The number is not exact because some of the arrays dimensions are set based on the number of nodes on the open boundary and the coastline, which are very domain specific. In order to obtain an executable that will handle a larger number of nodes, contact technical support at Aquaveo. Larger executables are often posted on their ftp site.
It should be noted that due to the limitation of static arrays, the size of model that can be evaluated on a Windows PC is limited to a maximum of around 2,500,000 nodes. Be warned that running such a large model on a PC may take an extended period of time (possibly days).
With the availability of 64-bit machines, it is possible to access larger amounts of memory. However, this will not be an option for CGWAVE until the code is reworked to support dynamic arrays and tested on 64-bit machines.
Theoretical Basis / Mathematical Details
Additional Documents:
- Simulation of Waves in Harbors Using Two-Dimensional Elliptic Equation Models [1]
- Solution of the Mild-Slope Wave Problem by Iteration [2]
- A Finite Element Model for Wave Refraction and Diffraction. Tsay, T.-K. & P.L.-F. Liu (1983). Appl. Ocean Res., v5, 1, 30-37.
- Simulation of Wave Breaking Effects in Two-Dimensional Elliptic Harbor Wave Models [3]
- Simulation of Waves at Duck (North Carolina) Using Two Numerical Models [4]
- Incorporating Rubble Mound Jetties in Elliptic Harbor Wave Models [5]
- Exterior Reflections in Elliptic Harbor Wave Models [6]
- Exterior Bathymetric Effects in Elliptic Harbor Wave Models [7]
- Improved Coastal Boundary Condition for Surface Water Waves [8]
- Outgoing Boundary Conditions for Finite-Difference Elliptic Water-Wave Models [9]
External Links:
- May 2007 Infra-Gravity Wave Input Toolbox (IGWT): User’s Guide [10]
- Aug 2005 The Usage of CGWAVE in SMS: A User's Guide[11]
- Mar 2004 How to Use CGWAVE with SMS:An Example for Tedious Creek Small Craft Harbor [12]
- Jun 2003 Tedious Creek Small Craft Harbor:CGWAVE Model Comparisons Between Existing and Authorized Breakwater Configurations[13]
- Aug 1998 CGWAVE: A Coastal Surface Water Wave Model of the Mild Slope Equation [14]
Related Topics
SMS – Surface-water Modeling System | ||
|---|---|---|
| Modules: | 1D Grid • Cartesian Grid • Curvilinear Grid • GIS • Map • Mesh • Particle • Quadtree • Raster • Scatter • UGrid |  |
| General Models: | 3D Structure • FVCOM • Generic • PTM | |
| Coastal Models: | ADCIRC • BOUSS-2D • CGWAVE • CMS-Flow • CMS-Wave • GenCade • STWAVE • WAM | |
| Riverine/Estuarine Models: | AdH • HEC-RAS • HYDRO AS-2D • RMA2 • RMA4 • SRH-2D • TUFLOW • TUFLOW FV | |
| Aquaveo • SMS Tutorials • SMS Workflows | ||