GMS:Building Solids and 3D Meshes with TINs: Difference between revisions

From XMS Wiki
Jump to navigationJump to search
No edit summary
No edit summary
Line 22: Line 22:
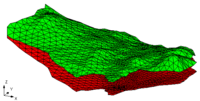
Boundaries are created around the perimeter of the solid and one large boundary is created at the base of the solid. The elevation of the horizontal plane is chosen so that the resulting solid is below the lowest point of interest. A series of two-dimensional cross sections of the primitive solids P, Q, and R formed by extruding the TINs in part a of the figure above is shown in part b.
Boundaries are created around the perimeter of the solid and one large boundary is created at the base of the solid. The elevation of the horizontal plane is chosen so that the resulting solid is below the lowest point of interest. A series of two-dimensional cross sections of the primitive solids P, Q, and R formed by extruding the TINs in part a of the figure above is shown in part b.


[[Image:extrusion.gif|frame|right|''3D TIN Extrusion (a) Surface Representing a Soil Interface Defined by a Triangulated Irregular Network. (b) Conversion of the Surface in (a) to a Solid by Extruding the Perimeter of the TIN.''|250px]]
[[Image:extrusion.gif|frame|right|''3D TIN Extrusion (a) Surface Representing a Soil Interface Defined by a Triangulated Irregular Network. (b) Conversion of the Surface in (a) to a Solid by Extruding the Perimeter of the TIN.''|200px]]
The final step of the modeling process consists of combining the primitive solids to form solid models of the soil layers. This is accomplished using set operations. Portions of the solids that overlap other solids are "trimmed" away and adjacent solids are forced to match precisely at the boundaries. This step of the modeling process is illustrated in part c. Primitive Q is subtracted from primitive P to produce the temporary solid P-Q. Primitive R is then subtracted from P-Q to produce the solid P'. The solid Q' is formed by subtracting primitive R from primitive Q. The primitive R does not intersect other solids and needs no trimming. Cross sections of the completed solid models of the soil layers are shown in part d.
The final step of the modeling process consists of combining the primitive solids to form solid models of the soil layers. This is accomplished using set operations. Portions of the solids that overlap other solids are "trimmed" away and adjacent solids are forced to match precisely at the boundaries. This step of the modeling process is illustrated in part c. Primitive Q is subtracted from primitive P to produce the temporary solid P-Q. Primitive R is then subtracted from P-Q to produce the solid P'. The solid Q' is formed by subtracting primitive R from primitive Q. The primitive R does not intersect other solids and needs no trimming. Cross sections of the completed solid models of the soil layers are shown in part d.


Revision as of 16:17, 23 June 2011

TIN Module
Tins.png
TINs
Creating a TIN
Editing a TIN
Converting TINS to Other Data Types
Building Solids and 3D Meshes with TINs
Map to MODFLOW with TINs
More
TIN Settings
TIN Display Options
TIN Tool Palette
TIN Commands
TIN Files
v • e

TINs can be used to build 3D solid models as well as 3D meshes. This can be done by selecting the following commands in the Build TIN menu:

  • Extrude TIN -> Solid - This command creates a new solid from each of the selected TINs by extruding each of the TINs up or down to an elevation specified by the user. Extruded TINs are useful in the construction of solid models of soil stratigraphy.
  • Fill Between TINs -> Solid - This command provides a quick way to create a solid bounded above and below by two or more selected TINs. The TIN defining the top of the boundary of the solid should be selected first. The remaining TIN(s) are then selected. All selected TINs are extruded down to an arbitrary elevation below that of all the selected TINs. GMS then performs a difference set operation .
  • Fill Between TINs -> 3D Mesh - A portion of a 3D finite element mesh can be constructed from two selected TINs using this command. Typically, the two TINs represent the top and bottom of a stratigraphic unit that is to be modeled with the 3D mesh. The two TINs should not intersect in order to use this command. Before using the this command it is first necessary to construct a 2D finite element mesh. When the command is selected, the user is prompted to input the number of mesh layers to be created between the TINs and to select the material type that will be associated with the new elements. A series of layers of 3D finite elements is then constructed between the two TINs by projecting each of the 2D elements in the 2D mesh. For example, if N layers are specified, N 3D wedge elements are created from each of the triangular elements in the 2D mesh, and N 3D hexahedral elements are created from each of the quadrilateral elements in the 2D mesh. The z coordinates of the nodes created for the 3D elements are distributed uniformly between the top and the bottom TINs.

The preferred method for creating solids is the Horizons method.

TINs can be used to build three-dimensional solid models of the soil layers. The transformation from TINs to solids is accomplished using a TIN extrusion and set operation procedure illustrated in two dimensions in the following figure. A two-dimensional cross section of three TINs, labeled p, q, and r, is shown in part a.

File:Stratigmod.gif
The TIN Extrusion and Set Operation Process. (a) Sample TINs. (b) Extrusion of Surfaces Into Solids. (c) Creation of Layers Through Set Operations. (d) Completed Solid Model of Soil Stratigraphy.

The TINs are converted into temporary solid primitives that represent approximations of the soil layers. The conversion is accomplished by projecting the outer boundary (perimeter) of each TIN down to a horizontal plane. This can be thought of as an extrusion process where a two-dimensional surface is extruded into a three-dimensional solid. A three-dimensional illustration of this process is shown in the figure below.

Boundaries are created around the perimeter of the solid and one large boundary is created at the base of the solid. The elevation of the horizontal plane is chosen so that the resulting solid is below the lowest point of interest. A series of two-dimensional cross sections of the primitive solids P, Q, and R formed by extruding the TINs in part a of the figure above is shown in part b.

File:Extrusion.gif
3D TIN Extrusion (a) Surface Representing a Soil Interface Defined by a Triangulated Irregular Network. (b) Conversion of the Surface in (a) to a Solid by Extruding the Perimeter of the TIN.

The final step of the modeling process consists of combining the primitive solids to form solid models of the soil layers. This is accomplished using set operations. Portions of the solids that overlap other solids are "trimmed" away and adjacent solids are forced to match precisely at the boundaries. This step of the modeling process is illustrated in part c. Primitive Q is subtracted from primitive P to produce the temporary solid P-Q. Primitive R is then subtracted from P-Q to produce the solid P'. The solid Q' is formed by subtracting primitive R from primitive Q. The primitive R does not intersect other solids and needs no trimming. Cross sections of the completed solid models of the soil layers are shown in part d.

The combination extrusion/set operation process can be simplified in some cases. For example, within GMS it is possible to create solid P' directly by "filling" between TIN p and the two TINs q and r. GMS accomplishes this by combining the process described above for creating solid P' into a single operation. The user simply selects TINs p, q, and r and performs the Fill Between TINs -> Solid command in the Build TINs menu of the TIN module.

The combination of TIN editing, TIN extrusion, and set operations represents a powerful and flexible tool that makes it possible to model complex stratigraphic relationships such as truncations, faults, embedded seams, and pinchout zones. Once the models are constructed, the volumes of the solids can be viewed using the Get Info command in the File menu. In addition, the models can be further modified using set operations to simulate complex excavations. Cross sections and fence diagrams can be constructed from the solid models at any location and at any orientation.

See also Solid Module; 3D mesh generation


v • e
GMS – Groundwater Modeling System
Modules:2D Grid  •  2D Mesh  •  2D Scatter Point  •  3D Grid  •  3D Mesh  •  3D Scatter Point  •  Boreholes  •  GIS  •  Map  •  Solid  •  TINs  •  UGridsGMS Logo2.png
Models:FEFLOW  •  FEMWATER  •  HydroGeoSphere  •   MODAEM  •  MODFLOW  •  MODPATH  •  mod-PATH3DU  •  MT3DMS  •  MT3D-USGS  •  PEST  •  PHT3D  •  RT3D  •  SEAM3D  •  SEAWAT  •  SEEP2D  •  T-PROGS  •  ZONEBUDGET
Aquaveo
Retrieved from "https://www.xmswiki.com/index.php?title=GMS:Building_Solids_and_3D_Meshes_with_TINs&oldid=34955"