GMS:Building Solids and 3D Meshes with TINs: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
*[[GMS:Horizons to 3D Mesh|'''Horizons -> 3D Mesh''']] | *[[GMS:Horizons to 3D Mesh|'''Horizons -> 3D Mesh''']] | ||
[[Image:stratigmod.gif|frame|right|''The TIN Extrusion and Set Operation Process. (a) Sample TINs. (b) Extrusion of Surfaces Into Solids. (c) Creation of Layers Through Set Operations. (d) Completed Solid Model of Soil Stratigraphy.'']] | |||
*'''Extrude TIN -> Solid''' - This command creates a new solid from each of the selected TINs by extruding each of the TINs up or down to an elevation specified by the user. Extruded TINs are useful in the construction of solid models of soil stratigraphy. | *'''Extrude TIN -> Solid''' - This command creates a new solid from each of the selected TINs by extruding each of the TINs up or down to an elevation specified by the user. Extruded TINs are useful in the construction of solid models of soil stratigraphy. | ||
| Line 15: | Line 16: | ||
TINs can be used to build three-dimensional solid models of the soil layers. The transformation from TINs to solids is accomplished using a TIN extrusion and [[GMS:Set Operations|set operation]] procedure illustrated in two dimensions in the following figure. A two-dimensional cross section of three TINs, labeled p, q, and r, is shown in part a. | TINs can be used to build three-dimensional solid models of the soil layers. The transformation from TINs to solids is accomplished using a TIN extrusion and [[GMS:Set Operations|set operation]] procedure illustrated in two dimensions in the following figure. A two-dimensional cross section of three TINs, labeled p, q, and r, is shown in part a. | ||
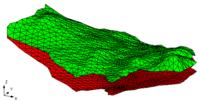
The TINs are converted into temporary solid primitives that represent approximations of the soil layers. The conversion is accomplished by projecting the outer boundary (perimeter) of each TIN down to a horizontal plane. This can be thought of as an extrusion process where a two-dimensional surface is extruded into a three-dimensional solid. A three-dimensional illustration of this process is shown in the figure below. | The TINs are converted into temporary solid primitives that represent approximations of the soil layers. The conversion is accomplished by projecting the outer boundary (perimeter) of each TIN down to a horizontal plane. This can be thought of as an extrusion process where a two-dimensional surface is extruded into a three-dimensional solid. A three-dimensional illustration of this process is shown in the figure below. | ||
| Line 22: | Line 21: | ||
Boundaries are created around the perimeter of the solid and one large boundary is created at the base of the solid. The elevation of the horizontal plane is chosen so that the resulting solid is below the lowest point of interest. A series of two-dimensional cross sections of the primitive solids P, Q, and R formed by extruding the TINs in part a of the figure above is shown in part b. | Boundaries are created around the perimeter of the solid and one large boundary is created at the base of the solid. The elevation of the horizontal plane is chosen so that the resulting solid is below the lowest point of interest. A series of two-dimensional cross sections of the primitive solids P, Q, and R formed by extruding the TINs in part a of the figure above is shown in part b. | ||
[[Image:extrusion.gif|frame| | [[Image:extrusion.gif|frame|left|''3D TIN Extrusion (a) Surface Representing a Soil Interface Defined by a Triangulated Irregular Network. (b) Conversion of the Surface in (a) to a Solid by Extruding the Perimeter of the TIN.''|200px]] | ||
The final step of the modeling process consists of combining the primitive solids to form solid models of the soil layers. This is accomplished using set operations. Portions of the solids that overlap other solids are "trimmed" away and adjacent solids are forced to match precisely at the boundaries. This step of the modeling process is illustrated in part c. Primitive Q is subtracted from primitive P to produce the temporary solid P-Q. Primitive R is then subtracted from P-Q to produce the solid P'. The solid Q' is formed by subtracting primitive R from primitive Q. The primitive R does not intersect other solids and needs no trimming. Cross sections of the completed solid models of the soil layers are shown in part d. | The final step of the modeling process consists of combining the primitive solids to form solid models of the soil layers. This is accomplished using set operations. Portions of the solids that overlap other solids are "trimmed" away and adjacent solids are forced to match precisely at the boundaries. This step of the modeling process is illustrated in part c. Primitive Q is subtracted from primitive P to produce the temporary solid P-Q. Primitive R is then subtracted from P-Q to produce the solid P'. The solid Q' is formed by subtracting primitive R from primitive Q. The primitive R does not intersect other solids and needs no trimming. Cross sections of the completed solid models of the soil layers are shown in part d. | ||