WMS:CE-QUAL-W2 Bathymetry
This article discusses the process WMS uses to compute bathymetric layer widths for CE-QUAL-W2 simulations. WMS is extremely useful for setting up CE-QUAL-W2 bathymetry files. WMS can also be used to setup CE-QUAL-W2 modeling parameters, but this page focuses only on the bathymetry file setup.
Laterally Averaged Finite Difference Grids
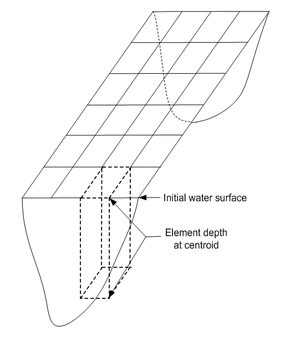
Most hydrodynamic models are depth-averaged, meaning that the numerical mesh (finite difference or finite element) is oriented in the x-y plane with each element representing a vertical column, or an average depth, of the domain being modeled. Tools for generating depth-averaged numerical models have been well developed because of the number of applications (Fugal, 2000; Thibodeaux, 1992; Gaspar et. al., 1994). Average depths for each element are determined by estimating an initial water surface level and then calculating the depth at each element centroid using bathymetric elevation data. The typical process requires defining a spatial domain of the model and then appropriately filling the regions with finite elements (quadrilaterals and/or triangles). Finally, a depth for each column is determined by calculating the difference between the assumed or starting water surface elevation of the element and the elevation determined from data gathered that describes the underlying bathymetry (see Figure 1).
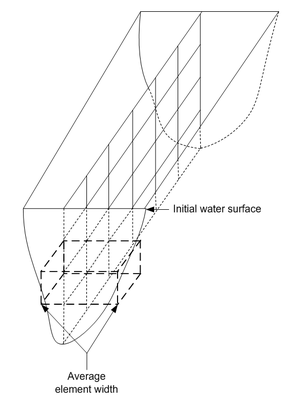
A major limitation of depth-averaged models is that they do not represent vertical variations well. For example, velocities computed using such a model do not account for variations that may occur between the top and bottom of the model since a single, average, value for each vertical column is computed. On the other hand, a laterally averaged numerical model better represents vertical variations, an important aspect of deeper water bodies such as lakes and reservoirs. However, in order to develop a laterally averaged numerical model an average width for each element must be determined. Unlike the depth-averaged models it is not possible to assume some initial “bank location” and then estimate the width to each element. Instead the bathymetry describing the shoreline elevations on either side of the model must be known so that a width at each element can be estimated as illustrated in Figure 2.
To develop the geometric representation for such models, discretization along the length and depth of the model must first be determined. In CE-QUAL-W2, segment lengths are determined from the spatial orientation of the water body. Tributary inflows, widening/narrowing of the water body and sampling or computational points are all indicators of how to divide the model up along its length into segments.
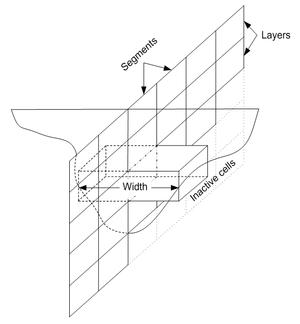
Layer depths are generally a function of the sensitivity, or gradient of the vertical variations of the variables being analyzed (i.e. temperature, phosphorous, dissolved oxygen, etc.). The higher the gradient the smaller the element heights should be. Once lengths and heights are determined a finite difference grid representing the profile of the water body can be constructed as shown in Figure 3. Cells are inactive if their centroid elevation drops below the bottom elevation of the water body. The final dimension required for the grid geometry of the model is an average width as illustrated in Figure 3.
Average widths are generally determined from the water body’s bathymetric data. This is the most difficult task in preparing the model geometry because each element width is unique (i.e. separate measurements required).
Estimating Average Widths
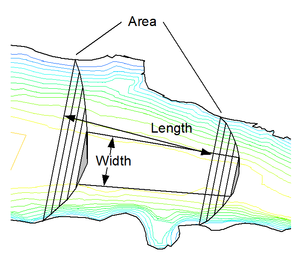
Widths are generally calculated from contours or sediment survey transects (cross sections) of the model bathymetry. In the case of contours a width is calculated by first determining the depth at the centroid of the segment at the layer and then measuring the distance at either side of the segment centerline to the contour with that elevation as shown in Figure 4.
Alternatively, transects at both ends of the element segment can be drawn until they intersect the contour at the centroid elevation. The area bounded by these contours and the segment ends determines a width calculated by dividing the area by the segment length. Even with excellent computer aided drawing (CAD) tools this is a tedious process and has prevented widespread use of such models, even though they are superior for problems in which vertical variations are important.
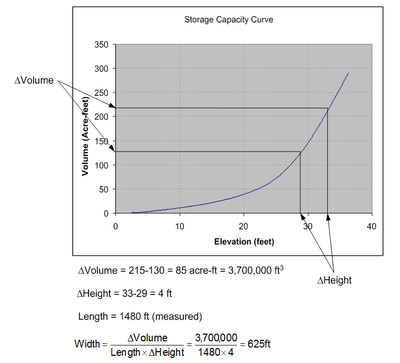
Most existing reservoirs have volume-elevation curves and/or area-elevation curves (referred to throughout the rest of this page as storage capacity curves) as part of their design. Such curves allow managers to quickly determine storage volumes or surface areas for a given water surface elevation. If a storage capacity curve for each of the model segments could be generated, computing element widths at the different layers within the segment would be straightforward and easy to automate in a computer algorithm. Once a volume is determined for an element centroidal depth the average width is easily computed from the three known quantities:
Figure 5 illustrates how volumes and a resulting segment width are determined for any given depth.
The key then to automating a process for developing geometric properties from bathymetric data is to develop a separate storage capacity curve for each of the model segments.
Storage Capacity Curve Generation From TIN
Triangulated Irregular Networks (TINs) are used by many programs to develop contours and compute other surface properties from scattered xyz elevation data (Lee and Schacter 1980, Watson 1981). A TIN is created by triangulating the xyz data points into a series of non-overlapping triangles which collectively form a piece-wise linear approximation of the surface. For CE-QUAL-W2 models, a TIN is used to compute a storage capacity curve for each segment.
Because a TIN is a piecewise linear representation of a surface, isolines can easily be computed for any given elevation. By bounding the TIN with the segment beginning and ending transects the area for any given contour elevation can be determined automatically. Any elevation interval can be chosen, but since the computations are automated with a computer algorithm a large number of areas (i.e. a small interval) for given elevations can be computed in a relatively short period of time generating a smooth elevation vs. area curve for the segment.
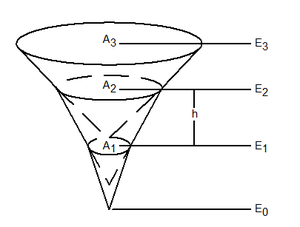
In order to compare with existing data typically developed during construction of a reservoir, a storage capacity curve (elevation vs. volume) is also determined using the conic method as outlined by the U.S. Army Corps of Engineers (HEC-1 1991). In the conic method incremental volumes between areas at elevations E1 and E2 (see Figure 6) are computed using the following equation:
Once a storage capacity curve is calculated (either elevation vs. area or elevation vs. volume), the widths are determined as described earlier (see Figure 5).
Implementation Using a Conceptual Modeling Approach
The algorithms to subdivide a TIN by segments and automate the calculation of a storage capacity curve for each segment have been implemented in the Watershed Modeling System (WMS) developed by the Environmental Modeling Research Laboratory (EMRL) of Brigham Young University with the cooperation of the Army Corps of Engineers (COE) Waterways Experiment Station (WES). The WMS is a modeling tool that supports geometric pre-processing of digital terrain data for several different watershed models including the COE’s CE-QUAL-W2 (W2). When developing a W2 model using the WMS, the lake, reservoir, or water body being modeled is first conceptually defined as a series of branches and segments (Smemoe et. al., 2000). An underlying digital terrain model representing the bathymetric elevations of the reservoir must be obtained. Wagner (2000) discusses several possible data sources for bathymetry elevations including: a gridded elevation matrix derived using a GPS and depth-finding device, digitization of contours from a topographic map that pre-dates the construction of the reservoir, and sediment survey transects. For newer reservoirs the USGS may have digital elevations already compiled. The bathymetric elevations must be defined for the extents of all segments in the W2 model.
The TIN representing the bathymetry of the entire water body is then subdivided into a separate TIN for each segment. A storage capacity curve for each segment is computed using the method described in the previous section. Layer depths are user-defined based on expected gradients and available computing resources. Finally, using the segment lengths, an estimate of the width at the mid point of each layer can be computed from the storage capacity curve of the given segment.
WMS further allows the definition of all of the CE-QUAL-W2 model components (Smemoe 2000), but the focus of this page is to discuss how the bathymetry data for a W2 (or a similar laterally averaged hydrodynamic model) model can be generated from a digital terrain model. The following case study illustrates this overall process.
Case Study
The purpose of the case study is to demonstrate how the algorithm for computing average widths in a laterally averaged finite difference model was implemented in the WMS software for creating CE-QUAL-W2 input files. The reservoir modeled is the East Canyon Reservoir located in northeastern Utah (See Figure 7).
East Canyon is a medium sized reservoir, containing a maximum storage of 6,200 acre*ft at the maximum water surface elevation (spillway invert). It is a shallow reservoir, averaging only 8 feet. The shallow depth combined with sources of reservoir inflows has caused chronic algal bloom problems. The Bureau of Reclamation, Salt Lake City office is currently undergoing an investigation into the existing TMDL using the CE-QUAL-W2 model. The WMS software was used to generate the grid parameters (known as the bathymetry input file in CE-QUAL-W2) for this model. The following generalized steps were used in WMS for creating a bathymetry file for the East Canyon Reservoir:
- Obtain underlying digital elevation data
- Determine the model boundary
- Verify the accuracy of the digital elevation data – adjust if necessary
- Determine the reservoir branches and segments
- Compute storage capacity curves for each model segment
- Calculate average widths for segment layers
Digital Elevation Data
The underlying digital elevation data used to create the bathymetry data (Figure 8) were derived from a high-resolution x-y-z data file of the reservoir bottom topography. For the East Canyon reservoir these data were created by making several passes with a depth-finding device that automatically recorded position and elevation.
Wagner (2000) discusses other possible methods for creating an underlying digital elevation file representing the topography of the bottom surface that includes digitizing a contour map and using transects from sediment surveys.
Determining the Model Boundary
For the East Canyon model the underlying digital elevation data included areas that were above the design or modeled water surface elevation. The maximum water surface elevation for the model was used to establish the model domain. In WMS this elevation can be contoured and the boundary traced to create a single polygon defining the model domain as shown in Figure 9.
Verifying the Underlying Digital Elevation Data
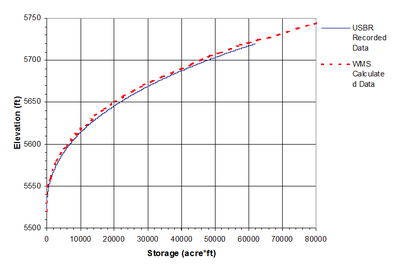
Before discretizing the model into a number of segments the accuracy of the elevations used to define the reservoir bottom are compared against the known storage capacity curve of the reservoir. Using WMS, a single storage capacity curve is derived from the bounding polygon created in the previous step and the underlying elevation data. This curve is then compared against the storage capacity curve for East Canyon developed from original surveys performed during the design and construction of the reservoir. The comparison is shown in the plot of Figure 10.
Even at the maximum water surface elevation the curves vary by less than 5% and so no further modifications were required. When using data sources such as sediment survey transects or less detailed contour maps it may be necessary to adjust the bathymetry by scaling as described in Wagner (2000).
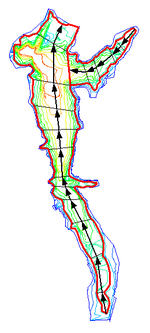
Determining Reservoir Branches and Segments
A CE-QUAL-W2 model is defined from a number of branches that are further subdivided into segments. The East Canyon reservoir was modeled as two branches as shown in Figure 11.
The primary branch was further subdivided into 12 segments and the tributary branch into 5 segments. In a CE-QUAL-W2 model the segments define the longitudinal dimension of the resulting finite difference grid.
Compute Storage Capacity Curves for Model Segments
In order to compute average widths for layers within a segment, a storage capacity curve for each segment must be derived. WMS does this as described earlier where the distance between elevations used to calculate the storage capacity curve is .1 unit (feet or meters depending on the units of the underlying digital elevation data). This establishes a smooth curve from the lowest elevation within the segment to the maximum water surface elevation and can be used to establish volumes between any two elevations as illustrated in Figure 5.
Calculate Average Widths for Segment Layers
The depth or layer dimension of the grid is established by the user and generally depends on the overall depth of the reservoir, gradients within the reservoir, and other model objective criteria. A layer depth of approximately 6 meters was used to construct the grid for this case study. The final grid dimension parameter required is the average width of each grid cell. The storage capacity curve for each segment was used to compute average widths using the storage capacity curve to determine the volumes between consecutive layer depth elevations and dividing by the product of the segment length and layer depth. A complete bathymetric description (lengths, depths and widths of all segments and layers) was developed for the full CE-QUAL-W2 model that is now being used by the Bureau of Reclamation in their TMDL analysis of the entire watershed.
Conclusion
CE-QUAL-W2 is a useful model for determining variations in temperature, dissolved oxygen, and other water quality parameters in reservoirs and other water bodies. Normally, most of the time spent in creating a CE-QUAL-W2 model is spent in building the laterally averaged finite difference grid and preparing the input files. The approach outlined in this page describes a method for estimating cell widths that makes the development of the grid manageable. The process is general enough to be used on any similar class of laterally averaged numerical models.
Acknowledgements
The text and pictures on this page were written by E. James Nelson (BYU), Douglas J. Gallup (Aquaveo), and Christopher M. Smemoe (Aquaveo). The information contained in this text is copyrighted by Aquaveo (2013).
Support from the Bureau of Reclamation and Army Corps of Engineers for this research is gratefully acknowledged. Insights gained through personal consultations with Tom Cole of the Waterways Experiment Station and Jerry Miller of the Salt Lake City Bureau of Reclamation office were instrumental in the development of this procedure.
References
- Nelson, E.J., N.L. Jones, and A.W. Miller, March 1994 "An algorithm for precise drainage basin delineation," ASCE Journal of Hydraulic Engineering, pp. 298-312.[1]
- Cole, T., “CE-QUAL-W2 Reference Manual,” Waterways Experiment Station, Vicksburg, Mississippi, 1995.
- Aquaveo, “WMS 9.1 User Manual,” 2013.
- Fugal, A.L., (2000). Two-Dimensional Finite Element Density Meshing, Masters Thesis, Brigham Young University, Provo, Utah.
- Gaspar, C., J. Jozsa, and J. Sarkkula, “Shallow Lake Modeling Using Quadtree-Based Grids,” International Conference on Computational Methods in Water Resources, vol 10, pp. 1053-1060, Heidelberg, 1994.
- Lee, D. T., and Schacter, B. J., 1980, "Two algorithms for constructing a Delauney triangulation," International Journal of Computer and Information Sciences, Vol. 9, No. 3 pp. 219-242.[2]
- Smemoe, Christopher M., E. James Nelson, and Tom Cole, “A Conceptual Modeling Approach to CE-QUAL-W2 Using the Watershed Modeling System,” Proceedings of the Hydroinformatics Conference, Iowa City, Iowa, July 2000.
- Thibodeaux, K.G., “Mesh-Generating Computer Program for the FESWMS-2DH Surface-Water Flow Model,” Hydraulic Engineering Water Forum, ASCE, 1992.[3]
- Wagner, Jason G., (2001). “Bathymetry Generation and Documentation for Water Quality Modeling”, Masters Project, Brigham Young University, Provo, Utah, 2001.
- Watson, D.F., 1981, "Computing the n-dimensional Delauney tessellation with application to Voronoi polytopes," The Computer Journal, Vol. 8, No. 2, pp. 167-172.[4]
WMS – Watershed Modeling System | ||
|---|---|---|
| Modules: | Terrain Data • Drainage • Map • Hydrologic Modeling • River • GIS • 2D Grid • 2D Scatter |  |
| Models: | CE-QUAL-W2 • GSSHA • HEC-1 • HEC-HMS • HEC-RAS • HSPF • MODRAT • NSS • OC Hydrograph • OC Rational • Rational • River Tools • Storm Drain • SMPDBK • SWMM • TR-20 • TR-55 | |
| Toolbars: | Modules • Macros • Units • Digitize • Static Tools • Dynamic Tools • Drawing • Get Data Tools | |
| Aquaveo | ||