GMS:Stochastic Modeling: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
|||
| (21 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Infobox Calibration}} | {{Infobox Calibration}} | ||
There are three methods in GMS for stochastic modeling using MODFLOW 2000 or 2005. The first, [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling|parameter zonation]], uses either a [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling| | There are three methods in GMS for stochastic modeling using MODFLOW 2000 or 2005. The first, [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling|parameter zonation]], uses either a [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling|random sampling]], a [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling|Latin hypercube sampling]], or [[GMS:Gaussian Field Generator|Gaussian fields]] to generate the different realizations. The second approach uses [[GMS:Stochastic Modeling#Using Indicator Simulations With Stochastic Modeling|indicator simulations]] generated by [[GMS:T-PROGS|T-PROGS]]. The third, the Null Space Monte Carlo (NSMC) method, generates multiple generated models with different sets of parameters (in GMS 9.0 and after). | ||
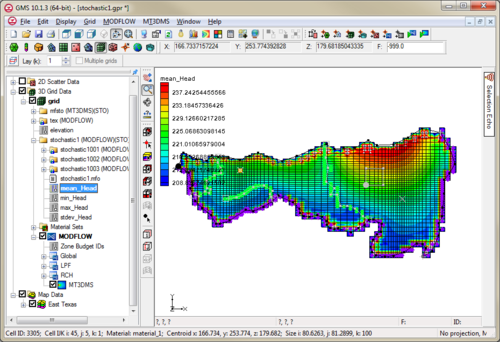
After the stochastic simulation results are generated, a user can view these results using the [[GMS:The GMS Window|Project Explorer]]. A user can also refine the results by using the [[GMS:Risk Analysis Wizard|''Risk Analysis Wizard'']] or [[GMS:Stochastic Modeling#Statistical Analysis of Stochastic MODFLOW/MT3D solutions| | After the stochastic simulation results are generated, a user can view these results using the [[GMS:The GMS Window|Project Explorer]]. A user can also refine the results by using the [[GMS:Risk Analysis Wizard|''Risk Analysis Wizard'']] or [[GMS:Stochastic Modeling#Statistical Analysis of Stochastic MODFLOW/MT3D solutions|statistical analysis of stochastic solutions]]. | ||
The stochastic modeling options can be added to a [http://www.aquaveo.com/software/gms-pricing paid edition] of GMS. | The stochastic modeling options can be added to a [http://www.aquaveo.com/software/gms-pricing paid edition] of GMS. | ||
| Line 14: | Line 14: | ||
==Stochastic Options Dialog== | ==Stochastic Options Dialog== | ||
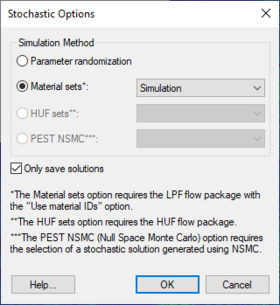
[[File:GMS StochasticOptions.png|thumb|280 px|The ''Stochastic Options'' dialog]] | [[File:GMS StochasticOptions.png|thumb|280 px|The ''Stochastic Options'' dialog]] | ||
Use the ''Stochastic Options'' dialog to select the type of stochastic simulation its major options. | Use the ''Stochastic Options'' dialog to select the type of stochastic simulation its major options. The dialog is reached through the ''MODFLOW'' | '''Stochastic''' menu command. | ||
''Parameter Randomization'' | |||
This option uses parameters defined in ''Parameters'' Dialog. | : This option uses parameters defined in ''Parameters'' Dialog. | ||
''Material Sets'' | |||
This option becomes available when there is at least one material set simulation in memory. One method for creating material sets is to use [[GMS:T-PROGS|T-PROGS]]. When this stochastic option is chosen, MODFLOW will be run once for each material set. This option also requires that the LPF package and the material IDs option be chosen. | : This option becomes available when there is at least one material set simulation in memory. One method for creating material sets is to use [[GMS:T-PROGS|T-PROGS]]. When this stochastic option is chosen, MODFLOW will be run once for each material set. This option also requires that the LPF package and the material IDs option be chosen. | ||
''HUF Sets'' | |||
This option becomes available when there is at least one HUF set simulation in memory. One method for creating HUF sets is to use [[GMS:T-PROGS|T-PROGS]]. When this stochastic option is chosen, MODFLOW will be run once for each HUF set. This option also requires that the HUF package be chosen. | : This option becomes available when there is at least one HUF set simulation in memory. One method for creating HUF sets is to use [[GMS:T-PROGS|T-PROGS]]. When this stochastic option is chosen, MODFLOW will be run once for each HUF set. This option also requires that the HUF package be chosen. | ||
''PEST NSMC'' | |||
: In order to use the Null Space Monte Carlo method, there must be a model that has already been calibrated using PEST with SVD-Assist. Selecting this option will cause an '''Options''' button to appear. This button will open the [[GMS:Null Space Monte Carlo|''Monte Carlo Options'']] dialog. | |||
Using this option requires less disk space, but doesn't allow loading and rerunning individual stochastic iteration simulations. | ''Only Save Solutions'' | ||
: With this option selected, during each stochastic iteration, changes are made to MODFLOW simulation and only a few files are saved. If this option is not selected, each stochastic iteration results in a new entire set of MODFLOW files being saved. | |||
: Using this option requires less disk space, but doesn't allow loading and rerunning individual stochastic iteration simulations. | |||
==Reading Stochastic Solutions== | ==Reading Stochastic Solutions== | ||
| Line 55: | Line 58: | ||
*[[GMS:Automated Parameter Estimation#4. Define Parameter Zones|Define parameters]] that link with the zones. | *[[GMS:Automated Parameter Estimation#4. Define Parameter Zones|Define parameters]] that link with the zones. | ||
*Select the ''Stochastic Simulation'' option from the [[GMS:Global Options/Basic Package|''Global Options'']] dialog. | *Select the ''Stochastic Simulation'' option from the [[GMS:Global Options/Basic Package|''Global Options'']] dialog. | ||
*Select the Parameter Randomization option from the ''Stochastic Options'' dialog. | *Select the ''Parameter Randomization'' option from the ''Stochastic Options'' dialog. | ||
*Choose whether to use the Random Sampling or Latin Hypercube randomization approaches in the ''Parameters'' dialog. | *Choose whether to use the ''Random Sampling'' or ''Latin Hypercube'' randomization approaches in the ''Parameters'' dialog. | ||
*Save and | *Save and run the model. | ||
*View the different model results using the [[GMS:The GMS Window|Project Explorer]]. | *View the different model results using the [[GMS:The GMS Window|Project Explorer]]. | ||
*Further analyze the results using the [[GMS:Risk Analysis Wizard|''Risk Analysis Wizard'']]. | *Further analyze the results using the [[GMS:Risk Analysis Wizard|''Risk Analysis Wizard'']]. | ||
| Line 63: | Line 66: | ||
=== Random Sampling === | === Random Sampling === | ||
Random | Random sampling is the most widely used approach for generating multiple random model simulations. GMS supports both normal and uniform distributions. | ||
A normal distribution can be defined as: | A normal distribution can be defined as: | ||
<!-- | <!--<math>f(x) = \dfrac{1}{\sqrt{2 \pi \sigma}} \text{exp} \left ( - \frac{(x-u)^2}{2 \sigma ^2} \right )</math>--> | ||
<math>f(x) = \dfrac{1}{\sqrt{2 \pi \sigma}} \text{exp} \left ( - \frac{(x-u)^2}{2 \sigma ^2} \right )</math>--> | :[[Image:stochasticeq1.jpg]] | ||
[[Image:stochasticeq1.jpg]] | |||
where σ is the standard deviation, μ is the mean, and x is the value being sampled. A uniform distribution can be defined as: | where σ is the standard deviation, μ is the mean, and x is the value being sampled. A uniform distribution can be defined as: | ||
<!-- | <!--<math>f(x) = \dfrac{1}{\beta - \alpha}</math>--> | ||
<math>f(x) = \dfrac{1}{\beta - \alpha}</math>--> | :[[Image:stochasticeq2.jpg]] | ||
[[Image:stochasticeq2.jpg]] | |||
where α and β are the bounds of the parameter value x. | where α and β are the bounds of the parameter value x. | ||
To set up the | To set up the random sampling, specify the mean, standard deviation, and upper and lower bounds for each parameter. Finally, choose how many realizations to generate. | ||
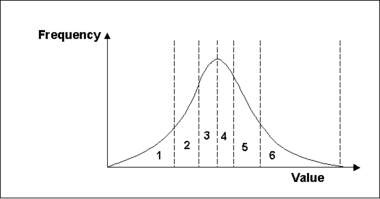
=== Latin Hypercube === | === Latin Hypercube === | ||
The Latin | The Latin hypercube randomization approach is a method that tries to efficiently probe the probability space for each parameter in a simulation in such a way that there is at least one simulation that represents every probability area for each parameter. | ||
First, specify the number of segments for each parameter. The total probability, defined by a distribution, mean, standard devation, and upper and lower bounds, is divided up into parts with equal probability (area). GMS then generates a random parameter value so that there is one value that lies within each probability segment. | First, specify the number of segments for each parameter. The total probability, defined by a distribution, mean, standard devation, and upper and lower bounds, is divided up into parts with equal probability (area). GMS then generates a random parameter value so that there is one value that lies within each probability segment. | ||
[[Image:freq. | [[Image:freq.png|thumb|none|380px]] | ||
This is repeated in a combinatorial fashion for each parameter so that there are | This is repeated in a combinatorial fashion for each parameter so that there are | ||
<!-- | <!--<math>\prod_{i=1}^n P_i</math>--> | ||
<math>\prod_{i=1}^n P_i</math>--> | :[[Image:stochasticeq3.jpg]] | ||
[[Image:stochasticeq3.jpg]] | |||
number of simulations, where n is the number of parameters and P is the number of segments for the ith parameter. For example, if there were three parameters with four, four, and five segments, the number of model runs would be as follows: | number of simulations, where n is the number of parameters and P is the number of segments for the ith parameter. For example, if there were three parameters with four, four, and five segments, the number of model runs would be as follows: | ||
<!-- | <!--<math>\ 4*4*5=80</math>--> | ||
<math>\ 4*4*5=80</math>--> | :[[Image:stochasticeq4.jpg]] | ||
[[Image:stochasticeq4.jpg]] | |||
Using the Latin | Using the Latin hypercube method has the benefit of needing a fewer number of runs to achieve the same level of confidence than the number required for the Monte Carlo approach because we have guaranteed that the entire probability range will be explored. | ||
==Using Indicator Simulations With Stochastic Modeling== | ==Using Indicator Simulations With Stochastic Modeling== | ||
| Line 108: | Line 107: | ||
*Generate Material Sets or HUF data using [[GMS:T-PROGS|T-PROGS]]. | *Generate Material Sets or HUF data using [[GMS:T-PROGS|T-PROGS]]. | ||
*Select the ''Stochastic Simulation'' from the [[GMS:Global Options/Basic Package|''Global Options'' | *Select the ''Stochastic Simulation'' from the [[GMS:Global Options/Basic Package|''Global Options'' dialog]]. | ||
*Enter the ''Stochastic...'' dialog from the ''MODFLOW'' menu. | *Enter the ''Stochastic...'' dialog from the ''MODFLOW'' menu. | ||
| Line 129: | Line 128: | ||
{{Navbox GMS}} | {{Navbox GMS}} | ||
[[Category:Stochastic]] | [[Category:Stochastic|Stochastic GMS]] | ||
[[Category:GMS Stochastic Modeling Dialogs]] | [[Category:GMS Stochastic Modeling Dialogs]] | ||
[[Category:Equations| | [[Category:Equations|Stochastic]] | ||