GMS:Stochastic Modeling: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
|||
| (59 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Infobox Calibration}} | {{Infobox Calibration}} | ||
There are | There are three methods in GMS for stochastic modeling using MODFLOW 2000 or 2005. The first, [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling|parameter zonation]], uses either a [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling|random sampling]], a [[GMS:Stochastic Modeling#Using Parameter Zonation With Stochastic Modeling|Latin hypercube sampling]], or [[GMS:Gaussian Field Generator|Gaussian fields]] to generate the different realizations. The second approach uses [[GMS:Stochastic Modeling#Using Indicator Simulations With Stochastic Modeling|indicator simulations]] generated by [[GMS:T-PROGS|T-PROGS]]. The third, the Null Space Monte Carlo (NSMC) method, generates multiple generated models with different sets of parameters (in GMS 9.0 and after). | ||
After the stochastic simulation results are generated, | After the stochastic simulation results are generated, a user can view these results using the [[GMS:The GMS Window|Project Explorer]]. A user can also refine the results by using the [[GMS:Risk Analysis Wizard|''Risk Analysis Wizard'']] or [[GMS:Stochastic Modeling#Statistical Analysis of Stochastic MODFLOW/MT3D solutions|statistical analysis of stochastic solutions]]. | ||
The stochastic modeling options can be added to a [http://www.aquaveo.com/software/gms-pricing paid edition] of GMS. | |||
[[Category:Link to Store]] | |||
==Stochastic Applications== | ==Stochastic Applications== | ||
One approach for dealing with model heterogeneity is stochastic simulations based on multiple equally plausible candidate realizations of the site heterogeneity. Ideally, such an approach would enable the generation of variability in subsurface soil stratigraphy based on interpretable geologic parameters such as lens width, material proportions, juxta-positioning tendencies and anisotropy. Multiple realizations that are conditioned to borehole data provide modelers with a rational approach for dealing with uncertainty associated with site characterization. Stochastic simulations can be applied to regional representations of the aquifer behavior in addition to local scale simulations. Stochastic simulations are particularly well-suited to local scale models since the resulting complex heterogeneity is more representative of actual stratigraphic deposition. This heterogeneity makes realistic and potentially more accurate contaminant transport simulation possible by simulating the preferential flow channels resulting from thin lenses of clays, sands, or other materials. The ultimate result of a stochastic approach is multiple simulations of hydraulic parameters that create a probabilistic solution. Such a solution has more credence and provides a better understanding of actual site conditions. | One approach for dealing with model heterogeneity is stochastic simulations based on multiple equally plausible candidate realizations of the site heterogeneity. Ideally, such an approach would enable the generation of variability in subsurface soil stratigraphy based on interpretable geologic parameters such as lens width, material proportions, juxta-positioning tendencies and anisotropy. Multiple realizations that are conditioned to borehole data provide modelers with a rational approach for dealing with uncertainty associated with site characterization. Stochastic simulations can be applied to regional representations of the aquifer behavior in addition to local scale simulations. Stochastic simulations are particularly well-suited to local scale models since the resulting complex heterogeneity is more representative of actual stratigraphic deposition. This heterogeneity makes realistic and potentially more accurate contaminant transport simulation possible by simulating the preferential flow channels resulting from thin lenses of clays, sands, or other materials. The ultimate result of a stochastic approach is multiple simulations of hydraulic parameters that create a probabilistic solution. Such a solution has more credence and provides a better understanding of actual site conditions. | ||
The ultimate application of T-PROGS is to generate stochastic simulations of soil heterogeneity. These realizations can then be incorporated into MODFLOW simulations as | The ultimate application of T-PROGS is to generate stochastic simulations of soil heterogeneity. These realizations can then be incorporated into MODFLOW simulations as "material sets" in the [[GMS:LPF Package|LPF package]] or as "HUF data" in the [[GMS:HUF Package|HUF package]]. (See [[GMS:T-PROGS|T-PROGS]]) | ||
==Stochastic Options Dialog== | |||
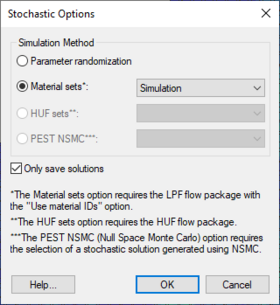
[[File:GMS StochasticOptions.png|thumb|280 px|The ''Stochastic Options'' dialog]] | |||
Use the ''Stochastic Options'' dialog to select the type of stochastic simulation its major options. The dialog is reached through the ''MODFLOW'' | '''Stochastic''' menu command. | |||
''Parameter Randomization'' | |||
: This option uses parameters defined in ''Parameters'' Dialog. | |||
''Material Sets'' | |||
: This option becomes available when there is at least one material set simulation in memory. One method for creating material sets is to use [[GMS:T-PROGS|T-PROGS]]. When this stochastic option is chosen, MODFLOW will be run once for each material set. This option also requires that the LPF package and the material IDs option be chosen. | |||
''HUF Sets'' | |||
: This option becomes available when there is at least one HUF set simulation in memory. One method for creating HUF sets is to use [[GMS:T-PROGS|T-PROGS]]. When this stochastic option is chosen, MODFLOW will be run once for each HUF set. This option also requires that the HUF package be chosen. | |||
''PEST NSMC'' | |||
: In order to use the Null Space Monte Carlo method, there must be a model that has already been calibrated using PEST with SVD-Assist. Selecting this option will cause an '''Options''' button to appear. This button will open the [[GMS:Null Space Monte Carlo|''Monte Carlo Options'']] dialog. | |||
''Only Save Solutions'' | |||
: With this option selected, during each stochastic iteration, changes are made to MODFLOW simulation and only a few files are saved. If this option is not selected, each stochastic iteration results in a new entire set of MODFLOW files being saved. | |||
: Using this option requires less disk space, but doesn't allow loading and rerunning individual stochastic iteration simulations. | |||
==Reading Stochastic Solutions== | |||
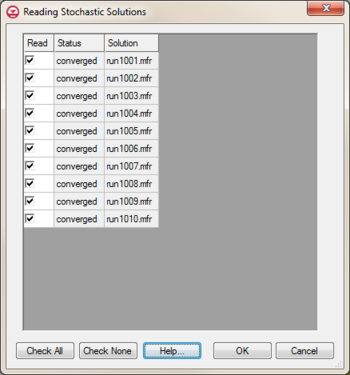
[[File:GMS - Reading Stochastic Solutions dialog.png|thumb|350 px|The ''Reading Stochastic Solutions'' dialog]] | |||
At the completion of the model run, if the ''Load Solution'' option is checked, the ''Reading Stochastic Solutions'' dialog will appear when exiting the model wrapper. This dialog gives the option to select which stochastic solutions to load into GMS. Solution not read in at this time can be opened at a later time. | |||
==Stochastic Inverse Modeling== | ==Stochastic Inverse Modeling== | ||
Stochastic inverse modeling is a [[GMS:Global Options/Basic Package|MODFLOW run option]] that takes each run in a stochastic simulation and performs [[GMS:Automated Parameter Estimation|parameter estimation]] on the run to find the optimal values based on observation data. This option is very time consuming compared with a regular stochastic simulation and a parameter estimation run because | Stochastic inverse modeling is a [[GMS:Global Options/Basic Package|MODFLOW run option]] that takes each run in a stochastic simulation and performs [[GMS:Automated Parameter Estimation|parameter estimation]] on the run to find the optimal values based on observation data. This option is very time consuming compared with a regular stochastic simulation and a parameter estimation run because GMS is doing parameter estimation for each stochastic run times. | ||
Stochastic inverse modeling can be performed only when using [[#Using Indicator Simulations With Stochastic Modeling|material sets or HUF arrays]] as chosen in the Stochastic Options dialog. [[GMS:Automated Parameter Estimation|PEST]] is the parameter estimation code supported by GMS. | Stochastic inverse modeling can be performed only when using [[GMS:Stochastic Modeling#Using Indicator Simulations With Stochastic Modeling|material sets or HUF arrays]] as chosen in the ''Stochastic Options'' dialog. [[GMS:Automated Parameter Estimation|PEST]] is the parameter estimation code supported by GMS. | ||
The following occurs during the stochastic inverse process: | The following occurs during the stochastic inverse process: | ||
| Line 23: | Line 51: | ||
The starting heads are interpolated to decrease the run times during the inverse portion. | The starting heads are interpolated to decrease the run times during the inverse portion. | ||
==Using Parameter Zonation With Stochastic Modeling== | ==Using Parameter Zonation With Stochastic Modeling== | ||
To create a stochastic MODFLOW simulation using parameter zonation, | To create a stochastic MODFLOW simulation using parameter zonation, follow these steps: | ||
*Further analyze the results using the [[GMS:Risk Analysis Wizard|Risk Analysis Wizard]]. | *First define the zones using key values. | ||
*[[GMS:Automated Parameter Estimation#4. Define Parameter Zones|Define parameters]] that link with the zones. | |||
*Select the ''Stochastic Simulation'' option from the [[GMS:Global Options/Basic Package|''Global Options'']] dialog. | |||
*Select the ''Parameter Randomization'' option from the ''Stochastic Options'' dialog. | |||
*Choose whether to use the ''Random Sampling'' or ''Latin Hypercube'' randomization approaches in the ''Parameters'' dialog. | |||
*Save and run the model. | |||
*View the different model results using the [[GMS:The GMS Window|Project Explorer]]. | |||
*Further analyze the results using the [[GMS:Risk Analysis Wizard|''Risk Analysis Wizard'']]. | |||
=== Random Sampling === | === Random Sampling === | ||
Random | Random sampling is the most widely used approach for generating multiple random model simulations. GMS supports both normal and uniform distributions. | ||
A normal distribution can be defined as: | A normal distribution can be defined as: | ||
<!-- | <!--<math>f(x) = \dfrac{1}{\sqrt{2 \pi \sigma}} \text{exp} \left ( - \frac{(x-u)^2}{2 \sigma ^2} \right )</math>--> | ||
<math>f(x) = \dfrac{1}{\sqrt{2 \pi \sigma}} \text{exp} \left ( - \frac{(x-u)^2}{2 \sigma ^2} \right )</math> | :[[Image:stochasticeq1.jpg]] | ||
where σ is the standard deviation, μ is the mean, and x is the value being sampled. A uniform distribution can be defined as: | where σ is the standard deviation, μ is the mean, and x is the value being sampled. A uniform distribution can be defined as: | ||
<!-- | <!--<math>f(x) = \dfrac{1}{\beta - \alpha}</math>--> | ||
<math>f(x) = \dfrac{1}{\beta - \alpha}</math> | :[[Image:stochasticeq2.jpg]] | ||
where α and β are the bounds of the parameter value x. | where α and β are the bounds of the parameter value x. | ||
To set up the | To set up the random sampling, specify the mean, standard deviation, and upper and lower bounds for each parameter. Finally, choose how many realizations to generate. | ||
=== Latin Hypercube === | === Latin Hypercube === | ||
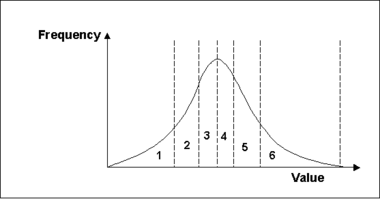
The Latin | The Latin hypercube randomization approach is a method that tries to efficiently probe the probability space for each parameter in a simulation in such a way that there is at least one simulation that represents every probability area for each parameter. | ||
First, | First, specify the number of segments for each parameter. The total probability, defined by a distribution, mean, standard devation, and upper and lower bounds, is divided up into parts with equal probability (area). GMS then generates a random parameter value so that there is one value that lies within each probability segment. | ||
[[Image:freq. | [[Image:freq.png|thumb|none|380px]] | ||
This is repeated in a combinatorial fashion for each parameter so that there are | This is repeated in a combinatorial fashion for each parameter so that there are | ||
[[Image: | <!--<math>\prod_{i=1}^n P_i</math>--> | ||
:[[Image:stochasticeq3.jpg]] | |||
number of simulations, where n is the number of parameters and P is the number of segments for the ith parameter. For example, if there were three | number of simulations, where n is the number of parameters and P is the number of segments for the ith parameter. For example, if there were three parameters with four, four, and five segments, the number of model runs would be as follows: | ||
[[Image: | <!--<math>\ 4*4*5=80</math>--> | ||
:[[Image:stochasticeq4.jpg]] | |||
Using the Latin | Using the Latin hypercube method has the benefit of needing a fewer number of runs to achieve the same level of confidence than the number required for the Monte Carlo approach because we have guaranteed that the entire probability range will be explored. | ||
==Using Indicator Simulations With Stochastic Modeling== | ==Using Indicator Simulations With Stochastic Modeling== | ||
GMS allows | GMS allows creating a stochastic simulation using output from T-PROGS. This can be in the form of either material sets or HUF data. Use the following steps: | ||
*Generate Material Sets or HUF data using [[GMS:T-PROGS|T-PROGS]]. | *Generate Material Sets or HUF data using [[GMS:T-PROGS|T-PROGS]]. | ||
*Select the Stochastic Simulation from the [[GMS:Global Options/Basic Package|Global Options | *Select the ''Stochastic Simulation'' from the [[GMS:Global Options/Basic Package|''Global Options'' dialog]]. | ||
*Enter the Stochastic... dialog from the MODFLOW menu. | *Enter the ''Stochastic...'' dialog from the ''MODFLOW'' menu. | ||
*Select the Material Sets option and choose the appropriate material set or HUF data simulation. | *Select the ''Material Sets'' option and choose the appropriate material set or HUF data simulation. | ||
*Save and Run MODFLOW. | *Save and Run MODFLOW. | ||
*View the different model results using the [[GMS:The GMS | *View the different model results using the [[GMS:The GMS Window|Project Explorer]]. | ||
*Further analyze the results using the [[GMS:Risk Analysis Wizard|Risk Analysis Wizard]]. | *Further analyze the results using the [[GMS:Risk Analysis Wizard|''Risk Analysis Wizard'']]. | ||
*GMS will generate as many MODFLOW runs as there are material sets. | *GMS will generate as many MODFLOW runs as there are material sets. | ||
==Statistical Analysis of Stochastic MODFLOW/ | ==Statistical Analysis of Stochastic MODFLOW/MT3DMS solutions== | ||
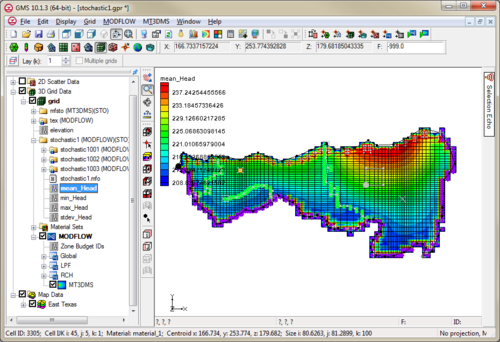
A statistical analysis can be computed on a Stochastic MODFLOW or | A statistical analysis can be computed on a Stochastic MODFLOW or MT3DMS solution by right-clicking on a stochastic folder in the [[GMS:Project Explorer|Project Explorer]] and selecting the '''Statistical Analysis''' command. This command creates four datasets for the mean, min, max, and standard deviation. The 3D grid display options can then be used to visualize these datasets. | ||
[[Image:StatAnalysis. | [[Image:StatAnalysis.png|thumb|none|left|500px|Stochastic statistical analysis example]] | ||
{{Navbox GMS}} | {{Navbox GMS}} | ||
[[Category:Stochastic]] | [[Category:Stochastic|Stochastic GMS]] | ||
[[Category:GMS Stochastic Modeling Dialogs]] | |||
[[Category:Equations|Stochastic]] | |||