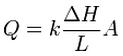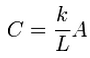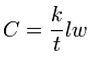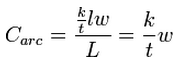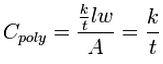|
|
| (27 intermediate revisions by 3 users not shown) |
| Line 7: |
Line 7: |
| Darcy's law states: | | Darcy's law states: |
|
| |
|
| <!--[[Image:eq_cond1.gif]]-->
| | [[Image:eq_cond1.png]] |
| <math>\ Q=kiA</math> | | <!--{{hide in print| <math>\ Q=kiA</math>}}--> |
|
| |
|
| | where: |
| | :''Q'' = flow rate [L^3/T] |
| | :''k'' = hydraulic conductivity [L/T] |
| | :''i'' = hydraulic gradient (unitless) |
| | :''A'' = gross cross-sectional area of flow [L^2]. |
|
| |
|
| where Q is the flow rate, k is the hydraulic conductivity, i represents the hydraulic gradient, and A represents the gross cross-sectional area of flow. Darcy's law can also be expressed as:
| |
|
| |
|
| <!--[[Image:eq_cond2.gif]]-->
| | Darcy's law can also be expressed as: |
| <math>\ Q=k \frac{\Delta H}{L} A</math>
| |
|
| |
|
| | [[Image:eq_cond2.png]] |
| | <!--<math>\ Q=k \frac{\Delta H}{L} A</math>--> |
|
| |
|
| where DH represents the head loss and L represents the length of flow. Since the unknown on the right side is the head, it is convenient to group all of the other terms together and call them conductance: | | where: |
| | :''ΔH'' = the head loss [L] |
| | :''L'' = the length of flow [L] |
|
| |
|
| <!--[[Image:eq_cond3.gif]]-->
| | |
| <math>\ Q=C \Delta H</math> | | Since the unknown on the right side is the head, it is convenient to group all of the other terms together and call them conductance: |
| | |
| | [[Image:eq_cond3.png]] |
| | <!--<math>\ Q=C \Delta H</math>--> |
| | |
| | where: |
| | : ''C'' = conductance [L^2/T] |
|
| |
|
|
| |
|
| This results in the following general definition for conductance: | | This results in the following general definition for conductance: |
|
| |
|
| <!--[[Image:eq_cond4.gif]]-->
| | [[Image:eq_cond4.png]] |
| <math>\ C= \frac{k}{L} A</math> | | <!--<math>\ C= \frac{k}{L} A</math>--> |
| | |
|
| |
|
| This may be represented more specifically in the following form. | | This may be represented more specifically in the following form. |
|
| |
|
| <!--[[Image:eq_cond5.gif]]-->
| | [[Image:eq_cond5.png]] |
| <math>\ C= \frac{k}{t} lw</math> | | <!--<math>\ C= \frac{k}{b} lw</math>--> |
|
| |
|
| | | where: |
| Where t represents the thickness of the material in the direction of flow, and lw represents the cross-sectional area perpendicular to the flow direction.
| | :''t'' = the thickness of the material in the direction of flow [L] |
| | :''lw'' = the cross-sectional area perpendicular to the flow direction [L^2]. |
|
| |
|
| == Conductance in conceptual models== | | == Conductance in conceptual models== |
| Line 42: |
Line 55: |
|
| |
|
| === Arcs === | | === Arcs === |
| | [[File:Arc-conductance.png|thumb|400 px|Arc conductance]] |
| Fortunately, GMS can automatically calculate the lengths of arcs and areas of polygons. Therefore, when a conductance is entered for an [[GMS:Feature Objects#Arcs|arc]], it should be entered in terms of '''conductance per unit length'''. For example, in the case of rivers, conductance should be entered as: | | Fortunately, GMS can automatically calculate the lengths of arcs and areas of polygons. Therefore, when a conductance is entered for an [[GMS:Feature Objects#Arcs|arc]], it should be entered in terms of '''conductance per unit length'''. For example, in the case of rivers, conductance should be entered as: |
|
| |
|
| <!--[[Image:eq_cond6.gif]]-->
| | [[Image:eq_cond6.png]] |
| <math>\ C_{arc}= \dfrac{\tfrac{k}{t} lw}{L} = \frac{k}{t} w</math> | | <!--<math>\ C_{arc}= \dfrac{\tfrac{k}{t} lw}{L} = \frac{k}{t} w</math>--> |
|
| |
|
| | where: |
| | :''C<sub>arc</sub>'' = conductance per unit length [(L^2/T)/L] or [L/T] |
| | :''t'' = the thickness of the material [L] |
| | :''w'' = the width of the material along the length of the arc [L] |
|
| |
|
| Where t is the thickness of the material and w is the width of the material along the length of the arc. When GMS applies the boundary condition from the arc to the grid cell, it automatically multiplies the entered value of conductance by the length of the arc that intersects the cell to create an accurate conductance value for the cell.
| | |
| | When GMS applies the boundary condition from the arc to the grid cell, it automatically multiplies the entered value of conductance by the length of the arc that intersects the cell to create an accurate conductance value for the cell. |
|
| |
|
| === Polygons === | | === Polygons === |
| For [[GMS:Feature Objects#Polygons|polygons]], conductance should be entered in a '''conductance per unit area''' form: | | For [[GMS:Feature Objects#Polygons|polygons]], conductance should be entered in a ''conductance per unit area'' form: |
| | |
| | [[Image:eq_cond7.png]] |
| | <!--<math>\ C_{poly}= \dfrac{\tfrac{k}{t} lw}{A} = \frac{k}{t} </math>--> |
|
| |
|
| <!--[[Image:eq_cond7.gif]]-->
| | where: |
| <math>\ C_{poly}= \dfrac{\tfrac{k}{t} lw}{A} = \frac{k}{t} </math> | | :''C<sub>poly</sub>'' = conductance per unit area [(L^2/T)/L^2] or [1/T] |
| | :''t'' = the thickness of the material [L] |
|
| |
|
|
| |
|
| Where t is the thickness of the material. When GMS converts the stress from a polygon to a grid cell, it automatically multiplies the entered value of conductance by the area of the cell that is covered by the polygon to create an appropriate conductance value for the cell. This restores the dimensional accuracy to the expression for conductance.
| | When GMS converts the stress from a polygon to a grid cell, it automatically multiplies the entered value of conductance by the area of the cell that is covered by the polygon to create an appropriate conductance value for the cell. This restores the dimensional accuracy to the expression for conductance. |
|
| |
|
| ===Points=== | | ===Points=== |
| Line 63: |
Line 86: |
|
| |
|
| ===Parameter Factors=== | | ===Parameter Factors=== |
| Beginning with GMS version 7.0, the Well, Drain, River, General head, and Stream boundary conditions have a parameter factor field that is associated with each boundary condition. The parameter factor is used with the parameter value to compute the final value of conductance for a given boundary condition (or in the case of the well package the final Q value). The parameter factor is automatically set by GMS when doing the Map-->MODFLOW command. This value will be set to the length of the arc in the cell or the area of the polygon in the cell associated with the boundary condition; for a point feature the factor is set to 1.0. | | Beginning with GMS version 7.0, the Well, Drain, River, General head, and Stream boundary conditions have a parameter factor field that is associated with each boundary condition. The parameter factor is used with the parameter value to compute the final value of conductance for a given boundary condition (or in the case of the well package the final Q value). The parameter factor is automatically set by GMS when doing the '''Map→MODFLOW''' command. This value will be set to the length of the arc in the cell or the area of the polygon in the cell associated with the boundary condition; for a point feature the factor is set to 1.0. |
| | |
| | ==See also== |
| | *[[GMS:Map to MODFLOW|Map to MODFLOW]] |
| | *[[GMS:MODFLOW Conceptual Model Approach|MODFLOW Conceptual Model Approach]] |
| | |
|
| |
|
| {{Navbox GMS}} | | {{Navbox GMS}} |
|
| |
|
| [[Category:MODFLOW]] | | [[Category:MODFLOW]] |
| | [[Category:Equations|Conductance]] |
| MODFLOW |
|---|
| Pre-processing |
|---|
|
MODFLOW Commands |
|
Building a MODFLOW Model |
|
Map to MODFLOW |
|
Calibration |
|
Packages Supported in GMS |
|
Saving a MODFLOW Simulation |
|
Importing MODFLOW Files |
|
Unsupported MODFLOW Features |
|
Run MODFLOW |
| Post-processing |
|---|
|
MODFLOW Display Options |
|
MODFLOW Post-Processing Viewing Options |
|
Reading a MODFLOW Simulation |
| Tutorials |
|---|
| Packages |
|---|
| Flow: |
BCF6, HUF, LPF, UPW |
|---|
| Solvers: |
DE4, GMG, NWT, PCG,
PCGN, LMG, SIP, SOR,
SMS |
|---|
| Other: |
BAS6, BFH, CHD1, CLN,
DRN1, DRT1, EVT1, ETS1,
GAGE, GHB1, GNC, HFB1,
HUF, LAK3, MNW1, MNW2,
OUT1, RCH1, RIV1, SFR2,
STR1, SUB1, SWI2, WEL1,
UZF1 |
|---|
|
Many MODFLOW boundary condition types (i.e., general head, rivers, streams, drains) include a conductance parameter. MODFLOW uses the conductance to determine the amount of water that flows in or out of the model due to the boundary condition stresses.
When using a conceptual model, the manner in which the conductance term should be computed and entered depends on whether the feature object is a polygon, arc or point. Before explaining this fully, a short review of the definition of conductance is appropriate.
Conductance formulation
Darcy's law states:
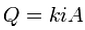
where:
- Q = flow rate [L^3/T]
- k = hydraulic conductivity [L/T]
- i = hydraulic gradient (unitless)
- A = gross cross-sectional area of flow [L^2].
Darcy's law can also be expressed as:
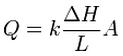
where:
- ΔH = the head loss [L]
- L = the length of flow [L]
Since the unknown on the right side is the head, it is convenient to group all of the other terms together and call them conductance:
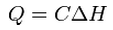
where:
- C = conductance [L^2/T]
This results in the following general definition for conductance:
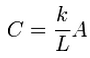
This may be represented more specifically in the following form.
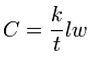
where:
- t = the thickness of the material in the direction of flow [L]
- lw = the cross-sectional area perpendicular to the flow direction [L^2].
Conductance in conceptual models
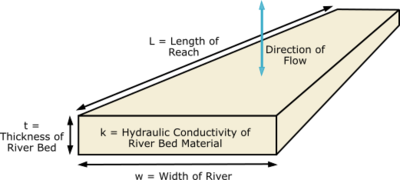
In the case of a river boundary condition, the conductance is defined in MODFLOW as the hydraulic conductivity of the river bed materials divided by the vertical thickness (length of travel based on vertical flow) of the river bed materials, multiplied by the area (width times the length) of the river in the cell. The last term, area, is the hardest parameter to determine by hand since it varies from cell to cell.
Arcs
Fortunately, GMS can automatically calculate the lengths of arcs and areas of polygons. Therefore, when a conductance is entered for an arc, it should be entered in terms of conductance per unit length. For example, in the case of rivers, conductance should be entered as:
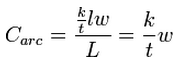
where:
- Carc = conductance per unit length [(L^2/T)/L] or [L/T]
- t = the thickness of the material [L]
- w = the width of the material along the length of the arc [L]
When GMS applies the boundary condition from the arc to the grid cell, it automatically multiplies the entered value of conductance by the length of the arc that intersects the cell to create an accurate conductance value for the cell.
Polygons
For polygons, conductance should be entered in a conductance per unit area form:
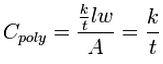
where:
- Cpoly = conductance per unit area [(L^2/T)/L^2] or [1/T]
- t = the thickness of the material [L]
When GMS converts the stress from a polygon to a grid cell, it automatically multiplies the entered value of conductance by the area of the cell that is covered by the polygon to create an appropriate conductance value for the cell. This restores the dimensional accuracy to the expression for conductance.
Points
When a general head, river, stream or drain attribute is assigned to an individual point, the conductance should be entered as a normal conductance value. This conductance is then directly assigned to the cell containing the point.
Parameter Factors
Beginning with GMS version 7.0, the Well, Drain, River, General head, and Stream boundary conditions have a parameter factor field that is associated with each boundary condition. The parameter factor is used with the parameter value to compute the final value of conductance for a given boundary condition (or in the case of the well package the final Q value). The parameter factor is automatically set by GMS when doing the Map→MODFLOW command. This value will be set to the length of the arc in the cell or the area of the polygon in the cell associated with the boundary condition; for a point feature the factor is set to 1.0.
See also