WMS:TIN Breaklines: Difference between revisions
No edit summary |
|||
| Line 6: | Line 6: | ||
Breakline Options option are controlled in the [[WMS:TIN Options|'''TIN Options''']] of the ''TINs'' menu. This dialog allows users to specify to either interpolate the z values from the existing TIN or to get the z values from feature arcs. The elevations of the new vertices are based on a linear interpolation of the breakline segments. The locations of the new vertices are determined in such a way that the Delauney criterion is satisfied. | Breakline Options option are controlled in the [[WMS:TIN Options|'''TIN Options''']] of the ''TINs'' menu. This dialog allows users to specify to either interpolate the z values from the existing TIN or to get the z values from feature arcs. The elevations of the new vertices are based on a linear interpolation of the breakline segments. The locations of the new vertices are determined in such a way that the Delauney criterion is satisfied. | ||
[[ | [[File:TIN ForcedBreakline.jpg]] | ||
==Related Topics== | ==Related Topics== | ||
Revision as of 15:51, 2 December 2015
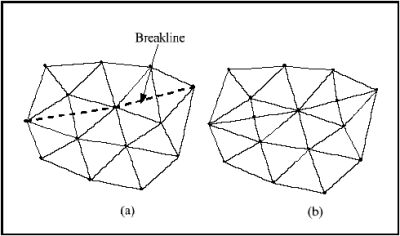
A breakline is a feature line or polyline representing a stream channel, ridge or some other feature to preserve in a TIN. In other words, a breakline is a series of edges that the triangles should conform to. Breaklines can be very useful when trying to eliminate unwanted pits on the interior of a TIN.
Breaklines can be processed using the Triangles | Insert Breakline(s) command from the TIN menu. Before selecting the command, one or more sequences of vertices defining the breakline(s) should be selected using the Select Vertices tool in the Tool Palette.
Breakline Options
Breakline Options option are controlled in the TIN Options of the TINs menu. This dialog allows users to specify to either interpolate the z values from the existing TIN or to get the z values from feature arcs. The elevations of the new vertices are based on a linear interpolation of the breakline segments. The locations of the new vertices are determined in such a way that the Delauney criterion is satisfied.
Related Topics
WMS – Watershed Modeling System | ||
|---|---|---|
| Modules: | Terrain Data • Drainage • Map • Hydrologic Modeling • River • GIS • 2D Grid • 2D Scatter |  |
| Models: | CE-QUAL-W2 • GSSHA • HEC-1 • HEC-HMS • HEC-RAS • HSPF • MODRAT • NSS • OC Hydrograph • OC Rational • Rational • River Tools • Storm Drain • SMPDBK • SWMM • TR-20 • TR-55 | |
| Toolbars: | Modules • Macros • Units • Digitize • Static Tools • Dynamic Tools • Drawing • Get Data Tools | |
| Aquaveo | ||