WMS:Triangulation
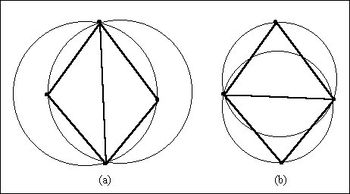
A TIN can be constructed by triangulating a set of vertices. WMS connects the vertices with a series of edges to form a network of triangles. The resulting triangulation satisfies the Delaunay criterion. The Delaunay criterion ensures that no vertex lies within the interior of any of the circumcircles of the triangles in the network (figure shown below).
As the triangulation process proceeds, adjacent triangles are compared to see if they satisfy the Delaunay criterion. If necessary, the adjacent edge of the two triangles is swapped (the diagonal of the quadrilateral defined by the two triangles is changed to the other two vertices) in order to satisfy the Delaunay criterion. This edge swapping process forms the basis of the triangulation algorithm.
When a new point is inserted into a TIN, the point is incorporated into the TIN and the edges of the triangles adjacent to the new point are swapped as necessary in order to satisfy the Delaunay criterion. If the Delaunay criterion is satisfied everywhere on the TIN, the minimum interior angle of all of the triangles is maximized. The result is that long thin triangles are avoided as much as possible.
It is important to note that the triangulation described above is used as a preliminary step to creating a TIN conditioned for basin delineation and is not sufficient in most cases for actually doing the drainage delineation. Even if beginning with TIN data, create another TIN using feature objects.
Triangulating
Vertices can be triangulated using the currently selected triangulation algorithm by selecting the Triangles | Triangulate command from the TIN menu. It is important to recognize that the Delaunay triangulation is not necessarily the best for performing drainage delineation because it does not ensure that important linear features such as streams and ridges will be honored in the TIN as triangle edges. For this reason, always use a TIN triangulated in this fashion as a "background" elevation source for creating a new TIN from a "conceptual" model of feature objects.
Triangulation Optimization
The Triangles | Optimize Triangulation command of the TIN menu will optimize triangulation according to the following criterion:
- If Angle Optimization is selected in the TIN Options dialog, the edges of triangles will be swapped to form edges that match the Delaunay criterion.
- If Area Optimization is selected in the TIN Options dialog, the edges of neighboring triangles will be swapped if the area of one triangle is more than the bias times the area of the smaller triangle.
The criteria is specified in the TIN Options dialog.
Remove Flat Triangles
The Triangles | Remove Flat Triangles command attempts to eliminate flat triangles on a TIN. A first pass is made in an attempt to adjust the triangulation or slightly alter vertex elevation and a second pass is then made which inserts new vertices in flat triangles and interpolates the elevation.
Interpolating Flat Triangles
This method inserts new points in flat triangles and adjusts the elevation of the new points by using an interpolation technique. This method works well when there is a small number of clustered (2-10) flat triangles. However, when large regions of flat triangles exist, the TIN filtering should be used before trying to remove flat objects.
When the Triangles | Remove Flat Triangles command in the TIN menu is issued, WMS computes the differences between the elevations of the flat triangles and the elevations of the surface defined by the IDW quadratic interpolation scheme. This technique is used because of its ability to accurately infer important terrain features such as pits, peaks, streams, and ridges. The difference between the flat surface and the interpolated surface is referred to as the "deviation" of the flat triangles. The deviation is computed at regularly spaced points on the interior of each flat triangle. The subdivision factor in the Interpolation Scheme dialog controls the level of subdivision or the number of interior points. The point in each flat triangle with the maximum deviation is assumed to represent the maximum for that triangle.
Once the deviations are determined, WMS locates the flat triangle whose deviation is the maximum. A new point is added at the XY location of the maximum deviation. The elevation of the new point is computed using the IDW quadratic interpolation scheme. The new point is inserted into the TIN, and the TIN is adjusted locally to accommodate the new point. Many times the insertion of a new point in a flat triangle combined with the local retriangulation of the TIN results in the removal of several flat triangles. The list of flat triangles is updated, the flat triangle with the next largest deviation is found, and the process is repeated. By inserting new points in this fashion, the minimum number of new points will be added in the best possible locations to infer local minima and maxima such as pits, peaks, streams, and ridges.
Once all flat triangles have been eliminated, further processing to remove flat edges and pits is done. Prior to performing the Triangles | Remove Flat Triangles command all TIN vertices are locked. Any new vertices created as part of this process are set to unlocked status. When completed, it is possible to distinguish the new vertices from the original by observing the ones that are unlocked. It may be desirable to unlock all vertices for further editing.
Boundary Triangles
The perimeter of the TIN resulting from the triangulation process corresponds to or approximates the convex hull of the data points. This may result in some long thin triangles or "slivers" on the perimeter of the triangulated region. There are several ways to deal with the long thin triangles.
Selecting Boundary Triangles
The thin triangles can be selected and deleted using the normal selection procedures. There is also an option for selecting thin triangles when the Select Triangles tool is selected. If the CTRL key is held down, it is possible to drag out a line with the mouse. All triangles intersecting the line will be selected.
Another technique can be used to select long thin triangles on the perimeter of the TIN. By selecting the Select Boundary Triangles command from the TIN menu, the thin triangles on the perimeter of the TIN are automatically selected.
The Select Boundary Triangles command checks triangles on the outer boundary first. If the length ratio of the triangle is less than the critical length ratio, the triangle is selected and the triangles adjacent to the triangle are then checked. The process continues inward until none of the adjacent triangles violate the minimum length ratio.
Thin Triangle Aspect Ratio
The critical length ratio for selecting thin triangles can be set by selecting Length Ratio from the TIN menu. The length ratio is defined as the longest side of the triangle divided by the sum of the two shorter sides.
A maximum edge length may also be specified in the TIN Options dialog.
Edge Swapping
TINs are generated in WMS using the Delaunay criteria. This method creates a set of triangles that are as equiangular as possible, and while this generally creates a good terrain surface, it does not ensure that all-important hydrologic features such as streams and ridges will be honored with triangle edges. A classic problem that occurs and inhibits drainage analysis is the "false dam". A false dam occurs during the triangulation process when an edge straddles a natural channel, forming a dam at the bottom of the channel as shown in Figure a. False dams are easily corrected by swapping the triangle edge ab to cd as illustrated in Figure b. Triangle edges are swapped using the Swap Edge tool and clicking on the edge which needs to be swapped.
Related Topics
- Creating TINs from Feature Objects
- TIN Options
- Trimming TINs
- Filtering TINs
- Smooth Pits
- Locked/Unlocked Vertices
- Interpolation Options
- Selecting Objects
- Delete
- Breaklines
- Creating Vertices
WMS – Watershed Modeling System | ||
|---|---|---|
| Modules: | Terrain Data • Drainage • Map • Hydrologic Modeling • River • GIS • 2D Grid • 2D Scatter |  |
| Models: | CE-QUAL-W2 • GSSHA • HEC-1 • HEC-HMS • HEC-RAS • HSPF • MODRAT • NSS • OC Hydrograph • OC Rational • Rational • River Tools • Storm Drain • SMPDBK • SWMM • TR-20 • TR-55 | |
| Toolbars: | Modules • Macros • Units • Digitize • Static Tools • Dynamic Tools • Drawing • Get Data Tools | |
| Aquaveo | ||