GMS:Risk Analysis Wizard: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 51: | Line 51: | ||
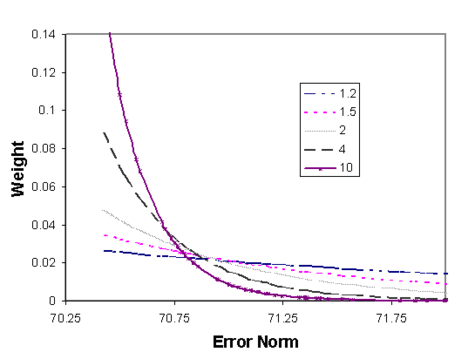
:In all of the capture zone methods, the algorithms used to synthesize the probability data set can be weighted using observation data. This makes it possible to give more weight to model instances with smaller calibration error when calculating the capture zone probabilities. The weighted head and flow observations can be compared to the computed values to come up with a global error norm, E, for each model run. This error norm can be based on the root mean squared (RMS) error, the sum of the squared weighted residuals, or any other measure selected by the modeler. For capture zone analysis, GMS uses the sum of squared weighted residuals (SSWR) for the error norm. The error norm from each MODFLOW run is used to compute a weight for the given solution using the following equation: | :In all of the capture zone methods, the algorithms used to synthesize the probability data set can be weighted using observation data. This makes it possible to give more weight to model instances with smaller calibration error when calculating the capture zone probabilities. The weighted head and flow observations can be compared to the computed values to come up with a global error norm, E, for each model run. This error norm can be based on the root mean squared (RMS) error, the sum of the squared weighted residuals, or any other measure selected by the modeler. For capture zone analysis, GMS uses the sum of squared weighted residuals (SSWR) for the error norm. The error norm from each MODFLOW run is used to compute a weight for the given solution using the following equation: | ||
<!-- | <!--<math>{\displaystyle w_i = \alpha ^ {\left [ \frac{ME-E_i}{SD} \right ]}}</math>--> | ||
<math>{\displaystyle w_i = \alpha ^ {\left [ \frac{ME-E_i}{SD} \right ]}}</math>--> | |||
::[[Image:riskwizardeq1.jpg]] ......................(1) | ::[[Image:riskwizardeq1.jpg]] ......................(1) | ||
:Where ''W<sub>i</sub>'' is the weight applied to solution ''i'', α is a user-defined factor, ''ME'' is the mean of the error values from all solutions, ''E<sub>jk</sub>'' is the error for solution ''i'', and ''SD'' is the standard deviation of error values from all solutions. The weights are also normalized as follows | :Where ''W<sub>i</sub>'' is the weight applied to solution ''i'', α is a user-defined factor, ''ME'' is the mean of the error values from all solutions, ''E<sub>jk</sub>'' is the error for solution ''i'', and ''SD'' is the standard deviation of error values from all solutions. The weights are also normalized as follows | ||
<!-- | <!--<math>{\displaystyle w_{final} = \frac{w_i}{\sum w_i}}</math>--> | ||
<math>{\displaystyle w_{final} = \frac{w_i}{\sum w_i}}</math>--> | |||
::[[Image:riskwizardeq2.jpg]] .......................(2) | ::[[Image:riskwizardeq2.jpg]] .......................(2) | ||
:so that the weights sum to unity. Equation 1 was developed to give the greater emphasis to the lower error values and to allow controlling the relative emphasis given to low vs. high values simply by adjusting the α value. The equation also avoids problems when one of the error values is zero, since a zero error value does not result in an infinite weight. The equation is also designed to allow scaling the weights according to the data being examined. This is done by subtracting the individual SSWR from the mean error and dividing by the standard deviation. | :so that the weights sum to unity. Equation 1 was developed to give the greater emphasis to the lower error values and to allow controlling the relative emphasis given to low vs. high values simply by adjusting the α value. The equation also avoids problems when one of the error values is zero, since a zero error value does not result in an infinite weight. The equation is also designed to allow scaling the weights according to the data being examined. This is done by subtracting the individual SSWR from the mean error and dividing by the standard deviation. | ||