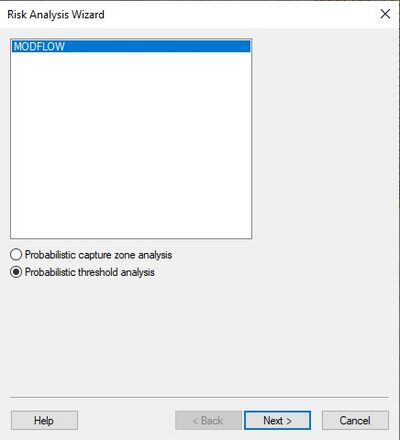
GMS:Risk Analysis Wizard: Difference between revisions
From XMS Wiki
Jump to navigationJump to search
| Line 28: | Line 28: | ||
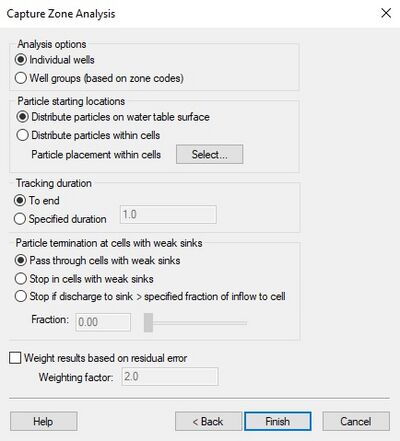
'''Analysis Options – Individual wells''' | '''Analysis Options – Individual wells''' | ||
:Choose this option to create a probabilistic capture zone for each uniquely named well in the MODFLOW model. | |||
Choose this option to create a probabilistic capture zone for each uniquely named well in the MODFLOW model. | |||
'''Analysis Options – Well groups''' | '''Analysis Options – Well groups''' | ||
:Choose this option to create a probabilistic capture zone for each different zone code number. | |||
Choose this option to create a probabilistic capture zone for each different zone code number. | |||
'''Particle Starting Locations – Distribute particles on water table surface''' | '''Particle Starting Locations – Distribute particles on water table surface''' | ||
:Choose this option to distribute particles only on the water table surface. By default, one particle is placed at the ''xy'' center of the cell at the water table, but the user can use the ''Particle placement within cells'' option to change the number of particles placed on the water table in each cell. This option will create a 2D probabilistic capture zone representing the intersection of the entire 3D probabilistic capture zone with the water table. | |||
Choose this option to distribute particles only on the water table surface. By default, one particle is placed at the ''xy'' center of the cell at the water table, but the user can use the ''Particle placement within cells'' option to change the number of particles placed on the water table in each cell. This option will create a 2D probabilistic capture zone representing the intersection of the entire 3D probabilistic capture zone with the water table. | |||
'''Particle Starting Locations – Distribute particles within cells''' | '''Particle Starting Locations – Distribute particles within cells''' | ||
:Choose this option to distribute particles within each cell. By default, one particle is placed at the center of each cell, but the user can use the ''Particle placement within cells'' option to change the number of particles placed on within each cell. This option creates three different probabilistic capture zones. The first represents the 3D capture zone, the other two represent different 2D projections of the 3D capture zone. | |||
Choose this option to distribute particles within each cell. By default, one particle is placed at the center of each cell, but the user can use the ''Particle placement within cells'' option to change the number of particles placed on within each cell. This option creates three different probabilistic capture zones. The first represents the 3D capture zone, the other two represent different 2D projections of the 3D capture zone. | |||
'''Tracking Duration – To end''' | '''Tracking Duration – To end''' | ||
:This option sets MODPATH to move particles through the flow field until they exit the model. | |||
This option sets MODPATH to move particles through the flow field until they exit the model. | |||
'''Tracking Duration – Specified duration''' | '''Tracking Duration – Specified duration''' | ||
:This option sets MODPATH to move particles through the flow field until they either exit the model or the time reaches the duration set, which ever comes first. | |||
This option sets MODPATH to move particles through the flow field until they either exit the model or the time reaches the duration set, which ever comes first. | |||
'''Particle Placement Within Cells''' | '''Particle Placement Within Cells''' | ||
:This option allows the user to change the number of particles per cell from the default of one. Increase the number of particles leads to a smoother capture zone, but drastically increases the computation time. | |||
This option allows the user to change the number of particles per cell from the default of one. Increase the number of particles leads to a smoother capture zone, but drastically increases the computation time. | |||
'''Weight Results Based On Residual Error''' | '''Weight Results Based On Residual Error''' | ||
:In all of the capture zone methods, the algorithms used to synthesize the probability data set can be weighted using observation data. This makes it possible to give more weight to model instances with smaller calibration error when calculating the capture zone probabilities. The weighted head and flow observations can be compared to the computed values to come up with a global error norm, E, for each model run. This error norm can be based on the root mean squared (RMS) error, the sum of the squared weighted residuals, or any other measure selected by the modeler. For capture zone analysis, GMS uses the sum of squared weighted residuals (SSWR) for the error norm. The error norm from each MODFLOW run is used to compute a weight for the given solution using the following equation: | |||
In all of the capture zone methods, the algorithms used to synthesize the probability data set can be weighted using observation data. This makes it possible to give more weight to model instances with smaller calibration error when calculating the capture zone probabilities. The weighted head and flow observations can be compared to the computed values to come up with a global error norm, E, for each model run. This error norm can be based on the root mean squared (RMS) error, the sum of the squared weighted residuals, or any other measure selected by the modeler. For capture zone analysis, GMS uses the sum of squared weighted residuals (SSWR) for the error norm. The error norm from each MODFLOW run is used to compute a weight for the given solution using the following equation: | |||
<!--[[Image:wt_eq.gif]] | <!--[[Image:wt_eq.gif]] | ||
| Line 63: | Line 55: | ||
[[Image:riskwizardeq1.jpg]] ......................(1) | [[Image:riskwizardeq1.jpg]] ......................(1) | ||
Where W<sub>i</sub> is the weight applied to solution i, [[Image:alpha_char.gif]] is a user-defined factor, ME is the mean of the error values from all solutions, E<sub>jk</sub> is the error for solution i, and SD is the standard deviation of error values from all solutions. The weights are also normalized as follows | :Where W<sub>i</sub> is the weight applied to solution i, [[Image:alpha_char.gif]] is a user-defined factor, ME is the mean of the error values from all solutions, E<sub>jk</sub> is the error for solution i, and SD is the standard deviation of error values from all solutions. The weights are also normalized as follows | ||
<!--[[Image:wt_final.gif]] | <!--[[Image:wt_final.gif]] | ||
<math>{\displaystyle w_{final} = \frac{w_i}{\sum w_i}}</math>--> | <math>{\displaystyle w_{final} = \frac{w_i}{\sum w_i}}</math>--> | ||
[[Image:riskwizardeq2.jpg]] .......................(2) | [[Image:riskwizardeq2.jpg]] .......................(2) | ||
:so that the weights sum to unity. Equation 1 was developed to give the greater emphasis to the lower error values and to allow the user to control the relative emphasis given to low vs. high values simply by adjusting the [[Image:alpha_char.gif]] value. The equation also avoids problems when one of the error values is zero, since a zero error value does not result in an infinite weight. We also wanted the equation to scale the weights according to the data being examined. This is done by subtracting the individual SSWR from the mean error and dividing by the standard deviation. | |||
:Equation 1 centers the weights on the mean error. The relative weight given to values differing from the mean is biased by the factor. This makes it possible to bias the resulting weight using knowledge of the site and the quality of the observation data. | |||
Equation 1 centers the weights on the mean error. The relative weight given to values differing from the mean is biased by the factor. This makes it possible to bias the resulting weight using knowledge of the site and the quality of the observation data. | |||
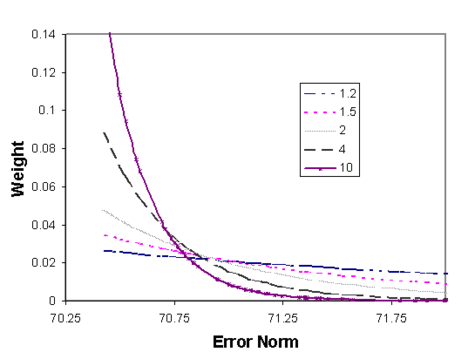
The figure below shows how the [[Image:alpha_char.gif]] factor in Equation 1 affects the weight applied to a given error. An [[Image:alpha_char.gif]] factor of 1.2 makes the contribution of each SSWR almost linear, whereas an [[Image:alpha_char.gif]] factor of ten gives most of the weight to the lowest 5-10 percent while discounting the other error values. We typically use an [[Image:alpha_char.gif]] value of 2.0. | :The figure below shows how the [[Image:alpha_char.gif]] factor in Equation 1 affects the weight applied to a given error. An [[Image:alpha_char.gif]] factor of 1.2 makes the contribution of each SSWR almost linear, whereas an [[Image:alpha_char.gif]] factor of ten gives most of the weight to the lowest 5-10 percent while discounting the other error values. We typically use an [[Image:alpha_char.gif]] value of 2.0. | ||
[[Image:wt_plot1. | :[[Image:wt_plot1.png|thumb|center|475 px|''Weight versus Error Norm Plot'']] | ||
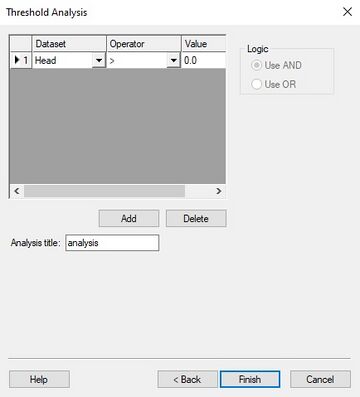
===Threshold Analysis Dialog=== | ===Threshold Analysis Dialog=== | ||