WMS:GSSHA Automated Calibration: Difference between revisions
No edit summary |
|||
| Line 24: | Line 24: | ||
===Defining Observed Data=== | ===Defining Observed Data=== | ||
[[Image:CalibrationObserved.jpg|thumb|right|550 px|Calibration ''GSSHA Observation'' dialog.]] | |||
Clicking the '''Observed Data...''' button in the ''Calibration Parameters'' dialog opens the [[WMS:GSSHA Observation Points|''GSSHA Observations'' dialog]] (below). In this dialog, enter in various types of observed data (including time series hydrograph data) for each event of the simulation. It is not necessary to associate a rainfall event with each observed data time series. | Clicking the '''Observed Data...''' button in the ''Calibration Parameters'' dialog opens the [[WMS:GSSHA Observation Points|''GSSHA Observations'' dialog]] (below). In this dialog, enter in various types of observed data (including time series hydrograph data) for each event of the simulation. It is not necessary to associate a rainfall event with each observed data time series. | ||
| Line 40: | Line 41: | ||
* Snow Water Equivalent | * Snow Water Equivalent | ||
* Tile Drain Discharge (in a GSSHA Storm Drain coverage) | * Tile Drain Discharge (in a GSSHA Storm Drain coverage) | ||
The [[WMS:GSSHA_Observation_Points|''GSSHA Observations'' dialog]] can be accessed from the feature point/node attribute dialog in the GSSHA and the GSSHA Storm Drain coverages. If WMS is running the default LM/SLM-based calibration, associate weights with each observation value in the XY series by clicking on the '''Weights''' button in the observation window and defining weights for each value. WMS defaults all the weights for observed data points to 1.0, but this value could be modified to give higher weights to certain observed values. | The [[WMS:GSSHA_Observation_Points|''GSSHA Observations'' dialog]] can be accessed from the feature point/node attribute dialog in the GSSHA and the GSSHA Storm Drain coverages. If WMS is running the default LM/SLM-based calibration, associate weights with each observation value in the XY series by clicking on the '''Weights''' button in the observation window and defining weights for each value. WMS defaults all the weights for observed data points to 1.0, but this value could be modified to give higher weights to certain observed values. | ||
| Line 65: | Line 64: | ||
**''Update Jacobian columns 0 to'' – Change the number of Jacobian columns | **''Update Jacobian columns 0 to'' – Change the number of Jacobian columns | ||
**''Use Tikhonov regularization'' – Turns Tikhonov regularization off or on. Tikhonov regularization provides a way to adjust the balance between fitting the solution to the observed data and fitting to the regularization relationships by defining a regularization weight factor and running Tikhonov regularization using this weight factor. The [http://gsshawiki.com/Alternate_Run_Modes:Efficient_Local_Search GSSHA wiki] has more information. | **''Use Tikhonov regularization'' – Turns Tikhonov regularization off or on. Tikhonov regularization provides a way to adjust the balance between fitting the solution to the observed data and fitting to the regularization relationships by defining a regularization weight factor and running Tikhonov regularization using this weight factor. The [http://gsshawiki.com/Alternate_Run_Modes:Efficient_Local_Search GSSHA wiki] has more information. | ||
**'''Advanced LM/SLM Parameters...''' – Brings up the [[#Advanced | **'''Advanced LM/SLM Parameters...''' – Brings up the [[#Advanced LM/SLM Parameters dialog|''Advanced LM/SLM Parameters'' dialog]]. | ||
*''Multistart parameters'' | *''Multistart parameters'' | ||
**'''Edit MS Parameters...''' – Brings up the ''Multistart Parameters'' dialog. | **'''Edit MS Parameters...''' – Brings up the [[#Multistart Parameters dialog|''Multistart Parameters'' dialog]]. | ||
*''Trajectory repulsion (TR) parameters'' | *''Trajectory repulsion (TR) parameters'' | ||
**'''Edit TR Parameters...''' – Brings up the ''Trajectory Repulsion (TR) Parameters'' dialog. | **'''Edit TR Parameters...''' – Brings up the [[#Trajectory Repulsion (TR) Parameters dialog|''Trajectory Repulsion (TR) Parameters'' dialog]]. | ||
*''Multilevel single linkage (MLSL) parameters'' | *''Multilevel single linkage (MLSL) parameters'' | ||
**'''Edit MLSL Parameters...''' – Brings up the ''Multilevel Single Linkage (MLSL) Parameters'' dialog. | **'''Edit MLSL Parameters...''' – Brings up the [[#Multilevel Single Linkage (MLSL) Parameters dialog|''Multilevel Single Linkage (MLSL) Parameters'' dialog]]. | ||
*''SCE parameters'' section | *''SCE parameters'' section | ||
**SCE is deprecated in GSSHA and is not supported beginning in WMS 10.0. | **SCE is deprecated in GSSHA and is not supported beginning in WMS 10.0. | ||
===Advanced | ===Advanced LM/SLM Parameters dialog=== | ||
[[Image:AdvancedLmSlmParameters.png|thumb|right|300 px|''Advanced LM/SLM Parameters'' dialog]] | [[Image:AdvancedLmSlmParameters.png|thumb|right|300 px|''Advanced LM/SLM Parameters'' dialog]] | ||
The ''Advanced LM/SLM Parameters'' dialog can be used to set advanced calibration settings when running an LM/SLM calibration. Some of the descriptions below were taken from the 2013 PEST User Manual. The following options are available in the ''Advanced LM/SLM Parameters'' section: | The ''Advanced LM/SLM Parameters'' dialog can be used to set advanced calibration settings when running an LM/SLM calibration. Some of the descriptions below were taken from the 2013 PEST User Manual. The following options are available in the ''Advanced LM/SLM Parameters'' section: | ||
| Line 91: | Line 90: | ||
*''NRELPAR'' – An integer variable. A value of "2" or "3" is often suitable. | *''NRELPAR'' – An integer variable. A value of "2" or "3" is often suitable. | ||
=== | ===Multistart Parameters dialog=== | ||
[[Image:GSSHA Multistart Parameters dialog.png|thumb|right|300 px|''Multistart Parameters'' dialog.]] | |||
The ''Multistart Parameters'' dialog has the following options: | |||
*''Random number seed'' – An integer used to initialize the random number generator. The random number generator's number sequence is determined by this seed. Therefore, if the same seed is used in additional runs, it will produce the same sequence of numbers. | |||
*''# of LM/SLM local searches'' – The number of LM/SLM local searches. A value of "3" is the default. | |||
{{-}} | |||
===Trajectory Repulsion (TR) Parameters dialog=== | |||
[[Image:GSSHA Trajectory Repulsion (TR) Parameters.png|thumb|right|300 px|''Trajectory Repulsion (TR) Parameters'' dialog.]] | |||
The ''Trajectory Repulsion (TR) Parameters'' dialog has the following options: | |||
*''Write random number seed file'' – Turn this on to export a random number seed file. | |||
*''Initial random number seed'' – An integer used to initialize the random number generator. The random number generator's number sequence is determined by this seed. Therefore, if the same seed is used in additional runs, it will produce the same sequence of numbers. | |||
*''# of initial function evaluations'' – An integer. The initial number of times to perform function evaluations. | |||
*''# of local searches'' – An integer. The number of local searches. A value of "3" is the default. | |||
*''# of local searches with no objective function improvement'' – An integer. The number of local searches to allow when no objective function improvement is obtained. A value of "2" is the default. | |||
*''Negligible objective function improvement fraction'' – A decimal fraction indicating the amount below which a function improvement is considered negligible. | |||
{{-}} | |||
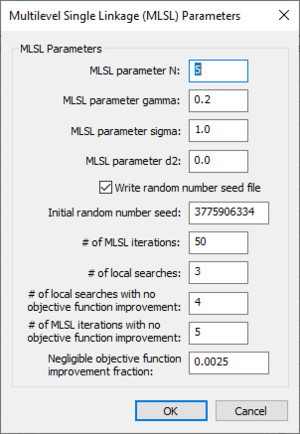
===Multilevel Single Linkage (MLSL) Parameters dialog=== | |||
[[Image:EditMlslParameters.png|thumb|right|300 px|''Multilevel Single Linkage (MLSL) Parameters'' dialog.]] | |||
The ''Multilevel Single Linkage (MLSL) Parameters'' dialog has the following options: | |||
*''MLSL parameter N'' – | |||
*''MLSL parameter gamma'' – | |||
*''MLSL parameter sigma'' – | |||
*''MLSL parameter d2'' – | |||
*''Write random number seed file'' – Turn this on to export a random number seed file. | |||
*''Initial random number seed'' – An integer. An integer used to initialize the random number generator. The random number generator's number sequence is determined by this seed. Therefore, if the same seed is used in additional runs, it will produce the same sequence of numbers. | |||
*''# of MLSL iterations'' – An integer. The number of MLSL iterations to include in the GSSHA run. | |||
*''# of local searches'' – An integer. The number of local searches. A value of "3" is the default. | |||
*''# of local searches with no objective function improvement'' – An integer. The number of local searches to allow when no objective function improvement is obtained. A value of "4" is the default. | |||
*''# of MLSL iterations with no objective function improvement'' – An integer. The number of MLSL iterations to allow when no objective function improvement is obtained. A value of "5" is the default. | |||
*''Negligible objective function improvement fraction'' – A decimal fraction indicating the amount below which a function improvement is considered negligible. | |||
{{-}} | |||
==Manual Calibration== | ==Manual Calibration== | ||
Revision as of 17:07, 11 April 2019
The GSSHA model allows for both automatic and manual calibration. There is WMS tutorial that describes how to set up a basic calibration model.
Automatic Calibration
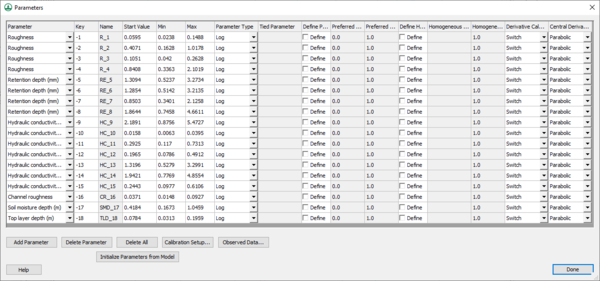
GSSHA has a PEST-based automated calibration routine, as described on the GSSHA wiki. WMS writes the parameters, observed data, and calibration files necessary to run GSSHA in any of the supported GSSHA calibration modes. Enter in the needed data by turning on Calibrate in the list on the right in the Job Control dialog.
Clicking on the Edit parameters button brings up the Parameters dialog (below) where parameters can be selected to be calibrated and edited, including the maximum, minimum, and initial values for each parameter.
Defining Key Values
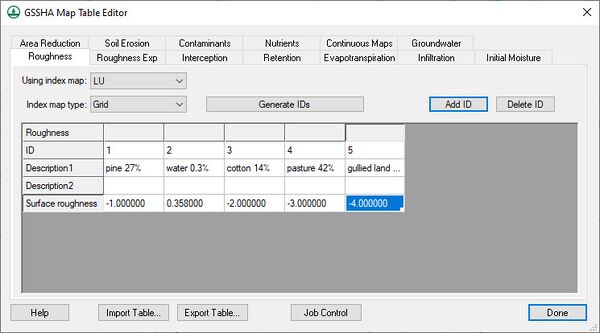
Select adjustable parameters by defining key values as negative integers in the regular GSSHA interface and then assigning starting, minimum, and maximum values to each of these parameters in the Parameters dialog. For example, to set overland Manning’s roughness values as an adjustable model parameter, specify negative integers for the values in the mapping table dialog as shown below:
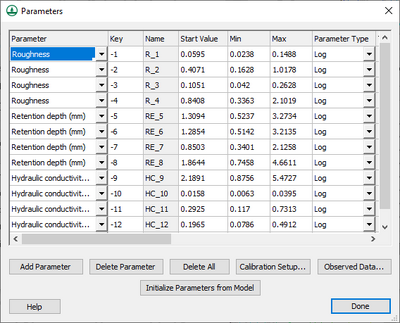
Then define the key values in the calibration Parameters dialog. The Initialize Parameters from Model button makes defining key values easy. This button searches the model for any parameters that are defined as negative integers and assigns these parameters to the dialog. Starting, minimum, and maximum values should be defined for each key value for the calibration engine. Other parameter information should also be defined, including:
- Whether parameters are fixed or tied to other parameters
- The methods used to calculate derivatives for each parameter
- Defining regularization parameters for prior calibration run information
- Defining preferred values (where a specific value is set as an optimal value for the calibration parameter) or homogeneous values (where one or more calibration parameters are linked to another calibration parameter in an attempt to get these values as close as possible).
Defining Observed Data
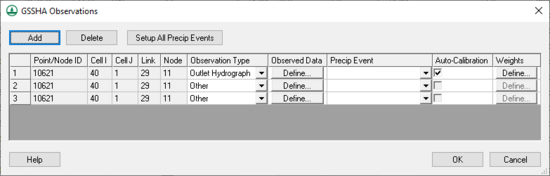
Clicking the Observed Data... button in the Calibration Parameters dialog opens the GSSHA Observations dialog (below). In this dialog, enter in various types of observed data (including time series hydrograph data) for each event of the simulation. It is not necessary to associate a rainfall event with each observed data time series.
This dialog shows all the feature points with observed data and allows turning automated calibration on or off for each of these observations. All automated calibration methods in WMS support automated calibration of the following data types at any computation point in the watershed model:
- Overland Depth
- Infiltration Depth
- Surface Moisture
- Grid Suspended Sediment (TSS) Concentration
- Channel Depth
- Channel Flow
- Channel Total Suspended Sediment (TSS) Concentration
- Groundwater Head
- Outlet Hydrograph (only at the watershed outlet point)
- Snow Water Equivalent
- Tile Drain Discharge (in a GSSHA Storm Drain coverage)
The GSSHA Observations dialog can be accessed from the feature point/node attribute dialog in the GSSHA and the GSSHA Storm Drain coverages. If WMS is running the default LM/SLM-based calibration, associate weights with each observation value in the XY series by clicking on the Weights button in the observation window and defining weights for each value. WMS defaults all the weights for observed data points to 1.0, but this value could be modified to give higher weights to certain observed values.
Defining Calibration Setup Parameters
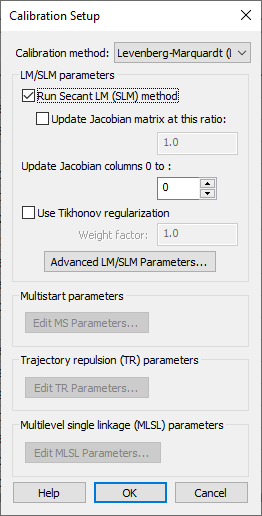
The calibration setup parameters are accessed by clicking the Calibration Setup... button to bring up the Calibration Setup dialog:
The parameters in this dialog are used for creating the calibration control file. This file, along with the parameters and observed data files are written out by WMS when saving a GSSHA project.
The following options are in this dialog:
- Calibration method – A drop-down with a list of calibration methods. The GSSHA wiki has more information on these methods.
- "Levenberg-Marquardt (LM)/Secant LM (SLM)" – Uses local search to optimize model parameters.
- "Multistart (MS)" – Uses global search to optimize model parameters.
- "Trajectory Repulsion (TR)" – Uses global search to optimize model parameters.
- "Multilevel Single Linkage (MLSL)" – Uses global search to optimize model parameters.
- LM/SLM parameters
- Run Secant LM (SLM) method – Turning on the option to run the SLM method sets the input file flag to run the SLM method instead of the LM (Levenberg-Marquardt) local search method. The SLM method is an efficiency enhancement to the LM method and is the default local search optimization method for a GSSHA calibration in the WMS interface.
- Update Jacobian matrix at this ratio – Allows adjusting of the Jacobian matrix update ratio.
- Update Jacobian columns 0 to – Change the number of Jacobian columns
- Use Tikhonov regularization – Turns Tikhonov regularization off or on. Tikhonov regularization provides a way to adjust the balance between fitting the solution to the observed data and fitting to the regularization relationships by defining a regularization weight factor and running Tikhonov regularization using this weight factor. The GSSHA wiki has more information.
- Advanced LM/SLM Parameters... – Brings up the Advanced LM/SLM Parameters dialog.
- Run Secant LM (SLM) method – Turning on the option to run the SLM method sets the input file flag to run the SLM method instead of the LM (Levenberg-Marquardt) local search method. The SLM method is an efficiency enhancement to the LM method and is the default local search optimization method for a GSSHA calibration in the WMS interface.
- Multistart parameters
- Edit MS Parameters... – Brings up the Multistart Parameters dialog.
- Trajectory repulsion (TR) parameters
- Edit TR Parameters... – Brings up the Trajectory Repulsion (TR) Parameters dialog.
- Multilevel single linkage (MLSL) parameters
- Edit MLSL Parameters... – Brings up the Multilevel Single Linkage (MLSL) Parameters dialog.
- SCE parameters section
- SCE is deprecated in GSSHA and is not supported beginning in WMS 10.0.
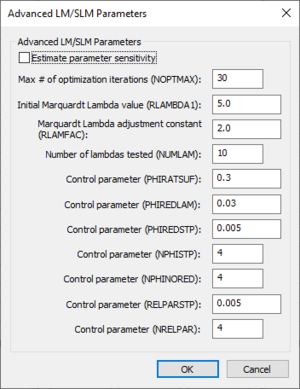
Advanced LM/SLM Parameters dialog
The Advanced LM/SLM Parameters dialog can be used to set advanced calibration settings when running an LM/SLM calibration. Some of the descriptions below were taken from the 2013 PEST User Manual. The following options are available in the Advanced LM/SLM Parameters section:
- Estimate parameter sensitivity – Turn this option on to write a "-1" to the NOPTMAX parameter in the PEST control file. This tells PEST to only run a sensitivity analysis instead of a full parameter optimization run. The sensitivity file is imported into WMS if reading the calibration solution.
- Max # of optimization iterations (NOPTMAX) – Sets the maximum number of optimization iterations that PEST is permitted to undertake on a particular parameter estimation run. To trigger PEST termination by other criteria more indicative of parameter convergence to an optimal set or of the futility of further processing, set this variable very high. A value of "20" to "30" is often appropriate.
If NOPTMAX is set to zero, PEST will not calculate the Jacobian matrix. Instead, it will terminate execution after just one model run. This setting can thus be used when calculating the objective function corresponding to a particular parameter set and/or to inspect observation residuals corresponding to that parameter set. - Initial Marquardt Lambda value (RLAMBDA1) – This real variable is the initial Marquardt lambda. PEST attempts parameter improvement using a number of different Marquardt lambdas during any one optimization iteration. However, in the course of the overall parameter estimation process, the Marquardt lambda generally gets smaller. An initial value of "1.0" to "10.0" is appropriate for most models.
Provide a higher initial Marquardt lambda if PEST complains that the normal matrix is not positive definite. For high values of the Marquardt lambda, the parameter estimation process approximates the steepest-descent method of optimization. While the latter method is inefficient and slow if used for the entirety of the optimization process, it often helps in getting the process started, especially if initial parameter estimates are poor. - Marquardt Lambda adjustment constant (RLAMFAC) – A real variable, and the factor by which the Marquardt lambda is adjusted. RLAMFAC must be greater than "1.0". When PEST reduces lambda, it divides by RLAMFAC; when it increases lambda, it multiplies by RLAMFAC. PEST reduces lambda if it can. However, if the normal matrix is not positive definite, or if a reduction in lambda does not lower the objective function, PEST has no choice but to increase lambda.
- Number of lanbdas tested (NUMLAM) – This integer variable places an upper limit on the number of lambdas that PEST can test during any one optimization iteration. It should normally be set between "5" and "10". For cases where parameters are being adjusted near their upper or lower limits, and for which some parameters are consequently being frozen (thus reducing the dimension of the problem in parameter space), a value closer to "10" may be more appropriate than one closer to "5". This gives PEST a greater chance of adjusting to the reduced problem dimension as parameters are frozen.
- PHIRATSUF – A real variable. Stands for "phi ratio sufficient". A value of "0.3" is often appropriate. If it is set too low, model runs may be wasted in search of an objective function reduction which it is not possible to achieve, given the linear approximation upon which the optimization equations are based. If it is set too high, PEST may not be given the opportunity of refining lambda in order that its value continues to be optimal as the parameter estimation process progresses.
During any one optimization iteration, PEST may calculate a parameter upgrade vector using a number of different Marquardt lambdas. First, it lowers lambda. If this is unsuccessful in lowering the objective function, it then raises lambda. At any stage, if it calculates an objective function which is a fraction PHIRATSUF or less of the starting objective function for that iteration, PEST considers the goal of the current iteration to have been achieved and moves on to the next optimization iteration. - PHIREDLAM – A real variable. A suitable value for PHIREDLAM is often around "0.01". If it is set too large, the criterion for moving on to the next optimization iteration is too easily met, and PEST is not given the opportunity of adjusting lambda to its optimal value for that particular stage of the PEST process. On the other hand, if PHIREDLAM is set too low, PEST will test too many Marquardt lambdas on each optimization iteration when it would be better off starting on a new iteration.
If a new/old objective function ratio of PHIRATSUF or less is not achieved, as the effectiveness of different Marquardt lambdas in lowering the objective function are tested, PEST must use some other criterion in deciding when it should move on to the next optimization iteration. This criterion is partly provided by PHIREDLAM. The first lambda that PEST employs in calculating the parameter upgrade vector during any one optimization iteration is the lambda inherited from the previous iteration, possibly reduced by a factor of RLAMFAC (unless it is the first iteration, in which case RLAMBDA1 is used). PEST will try another lambda unless PHIREDLAM reduces the objective function to less than PHIRATSUF of its value at the beginning of the iteration.
If the objective function is lower than for the first lambda (and still above PHIRATSUF of the starting objective function), PEST reduces lambda again. Otherwise, it increases lambda to a value greater by a factor of RLAMFAC than the first lambda for the iteration. When attempting to find a more effective lambda by lowering or raising lambda in this fashion, if the objective function begins to rise, PEST accepts the lambda and the corresponding parameter set. This gives rise to the lowest objective function for that iteration and moves on to the next iteration. If the relative reduction in the objective function between the use of two consecutive lambdas is less than PHIREDLAM, PEST determines it is more efficient to begin the next optimization iteration than to continue testing the effect of new Marquardt lambdas. - PHIREDSTP – A real variable used to tell PEST that the optimization process is at an end. For many cases, "0.01" is a suitable value.
- NPHISTP – An integer variable used to tell PEST that the optimization process is at an end. For many cases, "4" is a suitable value. Be careful to not set NPHISTP too low if the optimal values for some parameters are near or at their upper or lower bounds. This can cause the magnitude of the parameter upgrade vector to be curtailed over one or a number of optimization iterations to ensure that no parameter value overshoots its bounds. The result may then be smaller reductions in the objective function than would otherwise occur, which may mistakenly appear to be the onset of parameter convergence to the optimal set.
- NPHINORED – An integer variable. A value of "3" or "4" is often suitable. If PEST has failed to lower the objective function over NPHINORED successive iterations, it will terminate execution.
- RELPARSTP – A real variable. A value of "0.01" is often suitable. If the magnitude of the maximum relative parameter change between optimization iterations is less than RELPARSTP over NRELPAR successive iterations, PEST will terminate. PEST evaluates this change for all adjustable parameters at the end of each optimization iteration and determines the relative parameter change with the highest magnitude. If this maximum relative change is less than RELPARSTP, a counter is advanced by one. If it is greater than RELPARSTP, the counter is zeroed.
- NRELPAR – An integer variable. A value of "2" or "3" is often suitable.
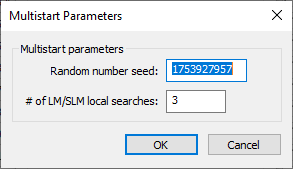
Multistart Parameters dialog
The Multistart Parameters dialog has the following options:
- Random number seed – An integer used to initialize the random number generator. The random number generator's number sequence is determined by this seed. Therefore, if the same seed is used in additional runs, it will produce the same sequence of numbers.
- # of LM/SLM local searches – The number of LM/SLM local searches. A value of "3" is the default.
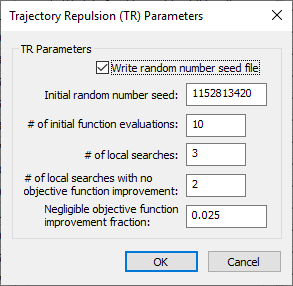
Trajectory Repulsion (TR) Parameters dialog
The Trajectory Repulsion (TR) Parameters dialog has the following options:
- Write random number seed file – Turn this on to export a random number seed file.
- Initial random number seed – An integer used to initialize the random number generator. The random number generator's number sequence is determined by this seed. Therefore, if the same seed is used in additional runs, it will produce the same sequence of numbers.
- # of initial function evaluations – An integer. The initial number of times to perform function evaluations.
- # of local searches – An integer. The number of local searches. A value of "3" is the default.
- # of local searches with no objective function improvement – An integer. The number of local searches to allow when no objective function improvement is obtained. A value of "2" is the default.
- Negligible objective function improvement fraction – A decimal fraction indicating the amount below which a function improvement is considered negligible.
Multilevel Single Linkage (MLSL) Parameters dialog
The Multilevel Single Linkage (MLSL) Parameters dialog has the following options:
- MLSL parameter N –
- MLSL parameter gamma –
- MLSL parameter sigma –
- MLSL parameter d2 –
- Write random number seed file – Turn this on to export a random number seed file.
- Initial random number seed – An integer. An integer used to initialize the random number generator. The random number generator's number sequence is determined by this seed. Therefore, if the same seed is used in additional runs, it will produce the same sequence of numbers.
- # of MLSL iterations – An integer. The number of MLSL iterations to include in the GSSHA run.
- # of local searches – An integer. The number of local searches. A value of "3" is the default.
- # of local searches with no objective function improvement – An integer. The number of local searches to allow when no objective function improvement is obtained. A value of "4" is the default.
- # of MLSL iterations with no objective function improvement – An integer. The number of MLSL iterations to allow when no objective function improvement is obtained. A value of "5" is the default.
- Negligible objective function improvement fraction – A decimal fraction indicating the amount below which a function improvement is considered negligible.
Manual Calibration
Manual calibration is the process of changing simulation input so that the simulation output matches observed values. Manual calibration takes a lot of experience and a lot of patience, but it is possible to achieve a good fit between the simulation and the observed data. Being able to successfully manually calibrate a simulation is a necessary skill to successfully set up and run an automatic calibration program.
Steps in the Manual Calibration Process
- Set up and run a successful simulation.
- Identify the calibration variables.
- Decide on a valid range for each variable.
- Set initial values of variables and run the model.
- Compare model results to observed values.
- Change variable values and re-run.
- Repeat steps 5 and 6 until the simulation results closely approximate the observed values.
1. Set up and run a successful simulation
The first step to calibrating a simulation is to set up and successfully run a reasonable simulation. All known parameters, such as precipitation, should be defined; all unknown parameters should be set to physically realistic values. For example, if actual roughness values are unknown then set all of the roughness values to 0.035 or some other reasonable number. Setting the roughness values to 0.00 or some default value will not allow the simulation to proceed. One important consideration is that if the spatial or temporal resolution is too coarse than the simulation will be unduly influenced by numerical issues related to the implementation of the partial differential equations. The result of too coarse of a temporal or spatial resolution will be delayed flows. For more information, see the Primer: Using Watershed Modeling System (WMS) for Gridded Surface Subsurface Hydrologic Analysis (GSSHA) Data Development – WMS 6.1 and GSSHA 1.43c (Downer et. al 2003).
2. Identify the calibration variables
The calibration variables are the simulation parameters whose exact quantities are unknown. This may range from a small handful to several dozen. At this stage it is also often necessary to identify which parameters the simulation is sensitive to and which can be left at good approximations without unduly affecting the model. The number of calibration variables must be pared down to a manageable number as well. Attempting to manually calibrate a simulation with dozens of unknown parameters will lead to one major headache and not to a good, robust simulation. Calibration cannot overcome a general lack of data.
Occasionally lab tests for such parameters as hydraulic conductivity will be available. Such data is very valuable but it still may be necessary to calibrate on that specific parameter because a simulation parameter represents a uniform parameter over an area while lab results generate the parameter for a specific point. The lab data is a very good starting value but may need some modification before it is applicable to a general area.
3. Decide on a valid range for each variable
Knowing a range for each variable is very important. To accurately simulate what is actually present in the watershed requires knowledge of the physical meaning of all of the numerical parameters for the watershed. Without this understanding a simulation that does not accurately reflect reality will be created and the simulation will be worthless in a predictive capacity. Consulting published works that describe the formulas used in GSSHA and detail the values and physical meaning of the formula parameters is highly recommended.
4. Set initial values of variables and run the model
Once the calibration variables have been decided upon and the valid range for each has been identified, the next step is to set an initial value for each variable. The usual process is to begin with the middle value. Later on these values will be modified little by little, either up or down. Beginning with the middle value of the range gives a good reference point for later simulations where what happens with a higher or lower value can be judged against the middle value to determine simulation trends.
5. Compare model results to observed values
This is the key step to calibrating a simulation. Click on the button in the Solution Results column of the Feature Point/Node Properties dialog to display the Solution Analysis dialog, which allows both visual inspection of the solution result as well as numerical evaluation of the “fitness” of a solution. Using these criteria judge how well the simulation output fits the observed.
6. Change variables and re-run
If the simulation output is not sufficiently close to the observed data then the next step is to adjust one or more of the model parameters to try to get a better fit. This step takes practice, experience, and patience. If by adjusting the variables outside of the predefined range a better fit is obtained then either the simulation is poorly set up or the data on which the model is based may be in question. It may also be that the interdependence of variables is such that the other variables in the model should be adjusted before the one that seems to call into question the parameter bounds. After adjusting the variables and running the simulation, check the new output and judge the results of the new variable setting.
Simulation non-uniqueness
One important facet of calibrating a simulation is that often changing more than one variable can have very similar results on the simulation output. Calibrating a simulation attempts to extract spatial simulation parameters from observed data through a process called inverse modeling. Problems arise in calibrating when modifying more than one variable produces only one type of result in the simulation. The question then arises as to which variable values should be the actual variable values. This problem is not solvable and the simulation is said to be non-unique or over-specified. The only way to overcome this problem is by utilizing more data that is of a different type than that already being used. For example, using a stream-flow hydrograph as well as a set of observed groundwater elevations would help eliminate simulation non-uniqueness.
GSSHA | |
|---|---|
| XMS Wiki Links | Calibration (Automated • Manual • Output) • Channel Routing • Contaminants • Digital Dams • Embankment Arcs • Feature Objects (Arcs • Nodes • Polygons) • File Types • Groundwater • Groups • Hydraulic Structures • Job Control • Join SSURGO Data • Mapping Tables • Maps • Menu • Model Linkage • Multiple Simulations • Nutrients • Observations • Output Control • Overland Soil Erosion • Pipe and Node Parameters • Precipitation • Radar Rainfall • Save GSSHA Project File • Smooth GSSHA Streams • Snowmelt • Solution (Analysis • Data) |
| Related Tools | MWBM Wizard • Using Soil Type Data with GSSHA |
| GSSHA Wiki External Links | GSSHA Wiki: Overview • Primer • User's Manual • Tutorials |
WMS – Watershed Modeling System | ||
|---|---|---|
| Modules: | Terrain Data • Drainage • Map • Hydrologic Modeling • River • GIS • 2D Grid • 2D Scatter |  |
| Models: | CE-QUAL-W2 • GSSHA • HEC-1 • HEC-HMS • HEC-RAS • HSPF • MODRAT • NSS • OC Hydrograph • OC Rational • Rational • River Tools • Storm Drain • SMPDBK • SWMM • TR-20 • TR-55 | |
| Toolbars: | Modules • Macros • Units • Digitize • Static Tools • Dynamic Tools • Drawing • Get Data Tools | |
| Aquaveo | ||